(本小题满分16分)在平面直角坐标系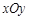 中,已知椭圆
中,已知椭圆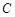 :
: 的离心率
的离心率 ,直线
,直线 过椭圆
过椭圆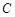 的右焦点
的右焦点 ,且交椭圆
,且交椭圆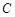 于
于 ,
, 两点.
两点.
(Ⅰ)求椭圆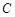 的标准方程;
的标准方程;
(Ⅱ)过点 作垂直于
作垂直于 轴的直线
轴的直线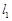 ,设直线
,设直线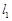 与定直线
与定直线 交于点
交于点 ,试探索当
,试探索当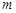 变化时,直线
变化时,直线 是否过定点?
是否过定点?
如图, 是棱长为1的正方体,四棱锥
是棱长为1的正方体,四棱锥 中,
中, 平面
平面 ,
,

(Ⅰ)求证:
(Ⅱ)求直线 与平面
与平面 所成角的正切值。
所成角的正切值。
已知 是等差数列,其n项和为
是等差数列,其n项和为 ,
,  ,
,
(Ⅰ)求 及
及 ;
;
(Ⅱ)令 ,求数列
,求数列 的前n项和
的前n项和
已知函数 .
.
(Ⅰ) 当 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(Ⅱ)设a,b,c分别为△ABC三个内角A,B,C的对边,f(C)=3,c=1,ab= ,求a,b的值。
,求a,b的值。
(本小题满分14分)
设函数 ,其中
,其中 .
.
( I )若函数 图象恒过定点P,且点P在
图象恒过定点P,且点P在 的图象上,求m的值;
的图象上,求m的值;
(Ⅱ)当 时,设
时,设 ,讨论
,讨论 的单调性;
的单调性;
(Ⅲ)在(I)的条件下,设 ,曲线
,曲线 上是否存在两点P、Q,
上是否存在两点P、Q,
使△OPQ(O为原点)是以O为直角顶点的直角三角形,且该三角形斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
(本小题满分12分)
如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且 已知椭圆D:
已知椭圆D: 的焦距等于
的焦距等于 ,且过点
,且过点

( I ) 求圆C和椭圆D的方程;
(Ⅱ) 若过点M斜率不为零的直线 与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补.
与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补.