已知 是等差数列,其n项和为
是等差数列,其n项和为 ,
,  ,
,
(Ⅰ)求 及
及 ;
;
(Ⅱ)令 ,求数列
,求数列 的前n项和
的前n项和
(本小题满分12分)已知椭圆C的中心为坐标原点O,焦点在y轴上,离心率 ,椭圆上的点到焦点的最短距离为
,椭圆上的点到焦点的最短距离为 , 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且
, 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且 .
.
(1)求椭圆方程;
(2)求 的取值范围.
的取值范围.
(本小题满分12分)已知直三棱柱 中,
中, ,
, ,点
,点 在
在 上.
上.
(1)若 是
是 中点,求证:
中点,求证: ∥平面
∥平面 ;
;
(2)当 时,求二面角
时,求二面角 的余弦值.
的余弦值.
(本小题满分12分)将编号为1,2,3,4的四张同样材质的卡片,随机放入编码分别为1,2,3,4的四个小盒中,每盒仅放一张卡片,若第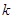 号卡片恰好落入第
号卡片恰好落入第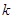 号小盒中,则称其为一个匹对,用
号小盒中,则称其为一个匹对,用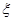 表示匹对的个数.
表示匹对的个数.
(1)求第2号卡片恰好落入第2号小盒内的概率;
(2)求匹对数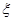 的分布列和数学期望
的分布列和数学期望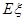 .
.
(本小题满分12分)
设函数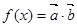 ,其中向量
,其中向量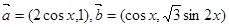 .
.
(1)求函数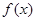 的最小正周期和在
的最小正周期和在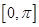 上的单调递增区间;
上的单调递增区间;
(2)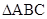 中,角
中,角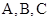 所对的边为
所对的边为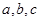 ,且
,且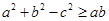 ,求
,求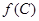 的取值范围.
的取值范围.
(本小题满分12分)已知公差大于零的等差数列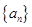 ,
,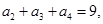 且
且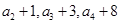 为等比数列
为等比数列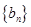 的前三项.
的前三项.
(1)求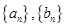 的通项公式;
的通项公式;
(2)设数列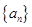 的前n项和为
的前n项和为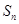 ,求
,求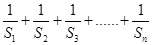 .
.