(本小题满分12分)如图四棱锥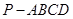 ,
,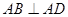 ,
,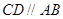 ,
,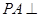 平面
平面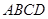 ,
,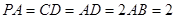 ,M为
,M为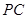 的中点.
的中点.
(Ⅰ)求证: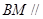 平面
平面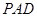 ;
;
(Ⅱ)在平面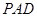 上找一点N,使得
上找一点N,使得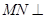 平面
平面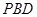 ;
;
(Ⅲ)求直线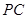 与平面
与平面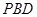 所成角的正弦.
所成角的正弦.
C.(选修4—4:坐标系与参数方程)
在极坐标系中,圆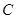 的方程为
的方程为 ,以极点为坐标原点
,以极点为坐标原点 ,极轴为
,极轴为 轴的正
轴的正
半轴建立平面直角坐标系,直线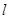 的参数方程为
的参数方程为 (
( 为参数),求直线
为参数),求直线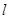 被
被 截
截
得的弦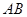 的长度.
的长度.
B.(选修4—2:矩阵与变换)
已知矩阵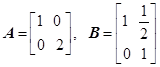 ,若
,若 矩阵
矩阵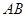 对应的变换把直线
对应的变换把直线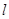 :
: 变为
变为
直线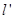 ,求直线
,求直线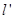 的方程.
的方程.
A.(选修4—1:几何证明选讲)
如图,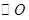 的半径
的半径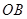 垂直于直径
垂直于直径 ,
,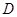 为
为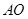 上一点,
上一点, 的延长线交
的延长线交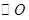 于点
于点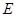 ,
,
过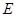 点的圆的切线交
点的圆的切线交
 的延长线于
的延长线于 .求证:
.求证: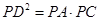 .
.
(本小题满分16分) [已知数列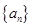 满足
满足 ,
,
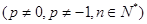 .
.
(1)求数列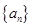 的通项公式
的通项公式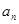 ;
;
(2)若对每一个正整数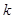 ,若将
,若将 按从小到大的顺序排列后,此三项均能构成等
按从小到大的顺序排列后,此三项均能构成等
差数列, 且公差为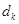 .①求
.①求 的值及对应的数列
的值及对应的数列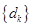 .
.
②记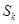 为数列
为数列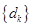 的前
的前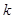 项和,问是否存在
项和,问是否存在 ,使得
,使得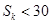 对任意正整数
对任意正整数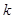 恒成立?若存
恒成立?若存
在,求出 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
(本小题满分16分)
对于函数 ,若存在实数对(
,若存在实数对(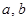 ),使得等式
),使得等式 对定义域中的每
对定义域中的每
一个 都成立,则称函数
都成立,则称函数
 是“(
是“(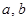 )型函数”.
)型函数”.
(1)判断函数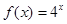 是否为“(
是否为“(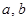 )型函数”,并说明理由;
)型函数”,并说明理由;
(2)已知函数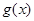 是“(1,4)型函数”, 当
是“(1,4)型函数”, 当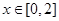 时,都有
时,都有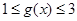 成立,且当
成立,且当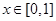
时,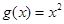
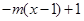
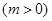 ,若,试求
,若,试求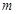 的取值范围.
的取值范围.