如图,某多面体的直观图及三视图如图所示: E,F分别为PC,BD的中点
(1)求证: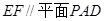
(2)求证:
(3)求此多面体的体积
直线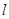 被两直线
被两直线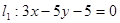 和
和 截得的线段中点为P
截得的线段中点为P
(1)求直线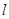 的方程
的方程
(2)已知点 ,在直线
,在直线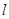 上找一点M,使
上找一点M,使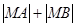 最小,并求出这个最小值
最小,并求出这个最小值
为了绿化城市,准备在如图所示的区域内修建一个矩形PQRC的草坪,且PQ//BC,RQ BC。另外
BC。另外 的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?
的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?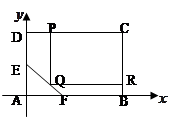
正三棱柱 中,E为AC中点
中,E为AC中点
(1)求证: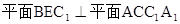
(2)求证: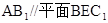 ,
,
已知直线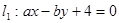 和直线
和直线 ,求分别满足下列条件的
,求分别满足下列条件的 的值
的值
(1) 直线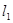 过点
过点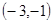 ,并且直线
,并且直线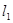 和
和 垂直
垂直
(2)直线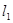 和
和 平行,且直线
平行,且直线 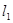 在
在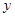 轴上的截距为-3
轴上的截距为-3