某股份有限公司根据公司实际情况,对本公司职工实行内部医疗公积金制度,公司规定:
(一)每位职工在年初需缴纳医疗公积金m元;
(二)职工个人当年治病花费的医疗费年底按表1的办法分段处理:
表1
| 分段方式 |
处理办法 |
| 不超过150元(含150元) |
全部由个人承担 |
| 超过150元,不超过10000元(不含150元,含10000元)的部分 |
个人承担n%,剩余部分由公司承担 |
| 超过10000元(不含10000元)的部分 |
全部由公司承担 |
设一职工当年治病花费的医疗费为x元,他个人实际承担的费用(包括医疗费个人承担的部分和缴纳的医疗公积金m元)为y元.
(1)由表1可知,当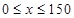 时,
时,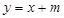 ;那么,当
;那么,当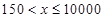 时,y = ;
时,y = ;
(用含m、n、x的方式表示)
(2)该公司职工小红和大明2014年治病花费的医疗费和他们个人实际承担的费用如表2:
| 职工 |
治病花费的医疗费x(元) |
个人实际承担的费用y(元) |
| 小红 |
300 |
280 |
| 大明 |
500 |
320 |
请根据表2中的信息,求m、n的值,并求出当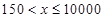 时,y关于x函数解析式;
时,y关于x函数解析式;
(3)该公司职工个人一年因病实际承担的费用最多只需要多少元?
数学课上,有这样一道探究题.
如图,已知 中, , , ,点 为平面内不与点 、 重合的任意一点,连接 ,将线段 绕点 顺时针旋转 ,得线段 ,连接 、 点 、 分别为 、 的中点,设直线 与直线 相交所成的较小角为 ,探究 的值和 的度数与 、 、 的关系.
请你参与学习小组的探究过程,并完成以下任务:
(1)填空:
【问题发现】
小明研究了 时,如图1,求出了 的值和 的度数分别为 , ;
小红研究了 时,如图2,求出了 的值和 的度数分别为 , ;
【类比探究】
他们又共同研究了 时,如图3,也求出了 的值和 的度数;
【归纳总结】
最后他们终于共同探究得出规律: (用含 、 的式子表示); (用含 的式子表示).
(2)求出 时 的值和 的度数.


如图,抛物线 与 轴交于 、 两点,与 轴交于点 ,对称轴 与 轴交于点 ,直线 ,点 是直线 上方抛物线上一动点,过点 作 ,垂足为 ,交 于点 ,连接 、 、 、 .
(1)抛物线的解析式为 ;
(2)当四边形 面积最大时,求点 的坐标;
(3)在(2)的条件下,连接 ,点 是 轴上一动点,在抛物线上是否存在点 ,使得以 、 、 、 为顶点,以 为一边的四边形是平行四边形.若存在,请直接写出点 的坐标;若不存在,说明理由.

如图,在菱形 中,对角线 、 相交于点 , 经过点 , ,交对角线 于点 ,且 ,连接 交 于点 .
(1)试判断 与 的位置关系,并说明理由;
(2)若 , ,求 的半径.

阅读理解:
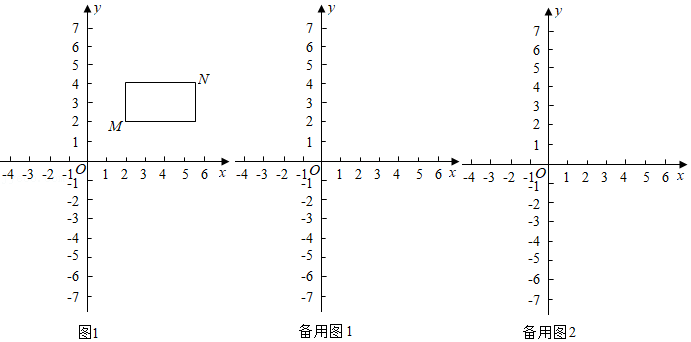
在平面直角坐标系中,点 的坐标为 , ,点 的坐标为 , ,且 , ,若 、 为某矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为 、 的"相关矩形".如图1中的矩形为点 、 的"相关矩形".
(1)已知点 的坐标为 .
①若点 的坐标为 ,则点 、 的"相关矩形"的周长为 ;
②若点 在直线 上,且点 、 的"相关矩形"为正方形,求直线 的解析式;
(2)已知点 的坐标为 ,点 的坐标为 若使函数 的图象与点 、 的"相关矩形"有两个公共点,直接写出 的取值.
为传承优秀传统文化,某地青少年活动中心计划分批次购进四大名著:《西游记》、《水浒传》、《三国演义》、《红楼梦》.第一次购进《西游记》50本,《水浒传》60本,共花费6600元;第二次购进《西游记》40本,《水浒传》30本,共花费4200元.
(1)求《西游记》和《水浒传》每本的售价分别是多少元;
(2)青少年活动中心决定再购买上述四种图书,总费用不超过32000元.如果《西游记》比《三国演义》每本售价多10元,《水浒传》比《红楼梦》每本售价少10元,要使先后购进的四大名著刚好配套(四大名著各一本为一套),那么这次最多购买《西游记》多少本?