中国“蛟龙”号深潜器目前最大深潜极限为7062.68米。某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°。
(1)沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;
(2)由于海流原因,“蛟龙”号需在B点处马上上浮,若平均垂直上浮速度为2000米/时,求“蛟龙”号上浮回到海面的时间。(参考数据: ≈1.414,
≈1.414, ≈1.732)
≈1.732)
解不等式 .
解:去分母,得 .
(1)请完成上述解不等式的余下步骤:
(2)解题回顾:本题“去分母”这一步的变形依据是 (填“ ”或“ ” .
.不等式两边都乘(或除以)同一个正数,不等号的方向不变;
.不等式两边都乘(或除以)同一个负数,不等号的方向改变.
计算:
(1) ;
(2) .
如图,二次函数 的图象与 轴交于点 ,过点 作 轴的平行线交抛物线于另一点 ,抛物线过点 ,且顶点为 ,连接 、 、 、 .
(1)填空: ;
(2)点 是抛物线上一点,点 的横坐标大于1,直线 交直线 于点 .若 ,求点 的坐标;
(3)点 在直线 上,点 关于直线 对称的点为 ,点 关于直线 对称的点为 ,连接 .当点 在 轴上时,直接写出 的长.

如图1, 与直线 相离,过圆心 作直线 的垂线,垂足为 ,且交 于 、 两点 在 、 之间).我们把点 称为 关于直线 的“远点“,把 的值称为 关于直线 的“特征数”.
(1)如图2,在平面直角坐标系 中,点 的坐标为 .半径为1的 与两坐标轴交于点 、 、 、 .
①过点 画垂直于 轴的直线 ,则 关于直线 的“远点”是点 (填“ ”.“ ”、“ ”或“ ” , 关于直线 的“特征数”为 ;
②若直线 的函数表达式为 .求 关于直线 的“特征数”;
(2)在平面直角坐标系 中,直线 经过点 ,点 是坐标平面内一点,以 为圆心, 为半径作 .若 与直线 相离,点 是 关于直线 的“远点”.且 关于直线 的“特征数”是 ,求直线 的函数表达式.
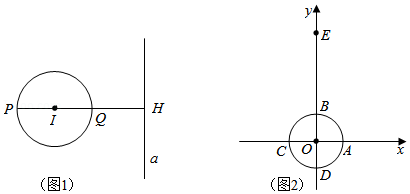
如图1,点 在线段 上, , , , .
(1)点 到直线 的距离是 ;
(2)固定 ,将 绕点 按顺时针方向旋转 ,使得 与 重合,并停止旋转.
①请你在图1中用直尺和圆规画出线段 经旋转运动所形成的平面图形(用阴影表示,保留画图痕迹,不要求写画法).该图形的面积为 ;
②如图2,在旋转过程中,线段 与 交于点 ,当 时,求 的长.
