(本小题满分12分)已知抛物线 ,直线
,直线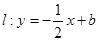 与抛物线交于
与抛物线交于 两点.
两点.
(1)若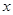 轴与以
轴与以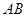 为直径的圆相切,求该圆的方程;
为直径的圆相切,求该圆的方程;
(2)若直线与 轴负半轴相交,求
轴负半轴相交,求 面积的最大值。
面积的最大值。
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x |
6 |
8 |
10 |
12 |
| y |
2 |
3 |
5 |
6 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ;
;
(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。
(相关公式: )
)
如图,在平行六面体ABCD-A1B1C1D1中,四边形ABCD与四边形CC1D1D均是边长为1的正方形,∠ADD1="120°" ,点E为A1B1的中点,点P,Q分别是BD,CD1上的动点,且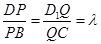 .
.
(1)当平面PQE//平面ADD1A1时,求 的值.
的值.
(2)在(1)的条件下,求直线QE与平面DQP所成角的正弦值.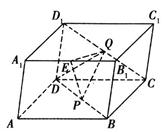
已知函数f(x)=4cosxsin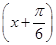 -1.
-1.
(1)求f(x)的最小正周期;
(2)求f(x)在区间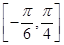 上的最大值和最小值.
上的最大值和最小值.
已知数列 的前n项和
的前n项和
(1)令 ,求证数列
,求证数列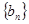 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
(2)令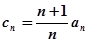 ,求数列
,求数列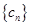 的前
的前 项和
项和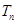 ;
;
(3)试比较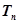 与
与 的大小(不需证明).
的大小(不需证明).
某企业生产 两种产品,每生产
两种产品,每生产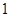 吨产品所需的劳动力、煤、电消耗及利润如下表:
吨产品所需的劳动力、煤、电消耗及利润如下表:
| 产品品种 |
劳动力(个) |
煤(吨) |
电(千瓦时) |
利润(万元) |
 产品 产品 |
4 |
9 |
3 |
7 |
 产品 产品 |
5 |
4 |
10 |
12 |
因条件限制,该企业仅有劳动力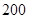 个,煤
个,煤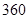 吨,供电局最多供电
吨,供电局最多供电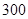 千瓦时,试问该企业生产
千瓦时,试问该企业生产 两种产品各多少吨时能获得最大利润?并求最大利润.
两种产品各多少吨时能获得最大利润?并求最大利润.