本题共有3小题,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分8分.
已知数列 是首项为3,公比为
是首项为3,公比为 的无穷等比数列,且数列
的无穷等比数列,且数列 各项的和等于9.对给定的
各项的和等于9.对给定的 ,设
,设 是首项为
是首项为 ,公差为
,公差为 的等差数列.
的等差数列.
(1)求数列 的通项
的通项 ;
;
(2)求数列 的前10项之和;
的前10项之和;
(3)设 为数列
为数列 的第
的第 项,
项, ,求
,求 ,并求正整数
,并求正整数 ,使得
,使得 存在且不等于零.
存在且不等于零.
设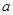 为实数,函数
为实数,函数 ,
,
(1)讨论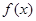 的奇偶性;
的奇偶性;
(2)当 时,求
时,求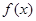 的最大值.
的最大值.
设
(1)试判断函数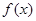 零点的个数;
零点的个数;
(2)若满足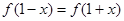 ,求m的值;
,求m的值;
(3)若m=1时, 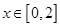 上存在
上存在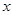 使
使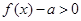 成立,求
成立,求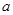 的取值范围.
的取值范围.
某机械生产厂家每生产产品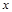 (百台),其总成本为
(百台),其总成本为 (万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本).销售收入
(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本).销售收入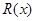 (万元)满足
(万元)满足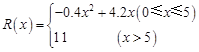 ,假定生产的产品都能卖掉,请完成下列问题:
,假定生产的产品都能卖掉,请完成下列问题:
(1)写出利润函数 的解析式;
的解析式;
(2)工厂生产多少台产品时,可使盈利最多?
已知函数 .
.
(1)设 的定义域为A,求集合A;
的定义域为A,求集合A;
(2)判断函数 在(1,+
在(1,+ )上单调性,并用单调性的定义加以证明.
)上单调性,并用单调性的定义加以证明.
已知函数 ,
,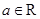 .
.
(1)若函数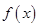 在
在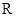 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(2)若存在实数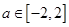 ,使得关于
,使得关于 的方程
的方程 有三个不相等的实数根,求实数
有三个不相等的实数根,求实数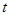 的取值范围.
的取值范围.