(本小题满分12分)某班元旦迎新有奖活动中有一节目,参与者同时掷出三个各面分别标有数字1,2,3,4,且质地均匀的小正四面体,规定:每位参与者只掷一次,取着地一面的数字,如果掷出所取的三个数字都不相同,如“1、2、3”,“1、2、4”等情形则为获奖.
(1)求某参与者获奖的概率;
(2)获奖一次得到十元的奖品,否则得到纪念奖2元的奖品,求甲、乙两位参与者总的奖品金额恰好为12元的概率.
已知函数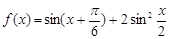 .
.
(1)求函数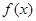 的单调递增区间;
的单调递增区间;
(2)记△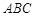 的内角
的内角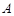 、
、 、
、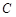 所对的边长分别为
所对的边长分别为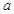 、
、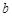 、
、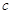 ,若
,若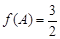 ,△
,△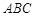 的面积
的面积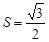 ,
,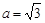 ,求
,求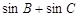 的值.
的值.
已知圆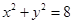 内有一点
内有一点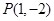 ,
, 为过点
为过点 且倾斜角为
且倾斜角为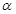 的弦,
的弦,
(1)当 时,求弦
时,求弦 的长.
的长.
(2)当弦 被点
被点 平分时,求出弦
平分时,求出弦 所在直线的方程.
所在直线的方程.
设 为关于n的k
为关于n的k 次多项式.数列{an}的首项
次多项式.数列{an}的首项 ,前n项和为
,前n项和为 .对于任意的正整数n,
.对于任意的正整数n, 都成立.
都成立.
(1)若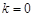 ,求证:数列{an}是等比数列;
,求证:数列{an}是等比数列;
(2)试确定所有的自然数k,使得数列{an}能成等差数列
若函数 为定义域
为定义域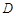 上单调函数,且存在区间
上单调函数,且存在区间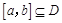 (其中
(其中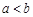 ),使得当
),使得当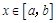 时,
时, 的取值范围恰为
的取值范围恰为 ,则称函数
,则称函数 是
是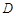 上的正函数,区间
上的正函数,区间 叫做等域区间.
叫做等域区间.
(1)已知 是
是 上的正函数,求
上的正函数,求 的等域区间;
的等域区间;
(2)试探究是否存在实数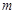 ,使得函数
,使得函数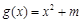 是
是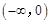 上的正函数?若存在,请求出实数
上的正函数?若存在,请求出实数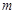 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
若椭圆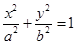 (
(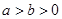 )过点
)过点 ,离心率为
,离心率为 ,
,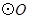 的圆心为原点,直径为椭圆的短轴,
的圆心为原点,直径为椭圆的短轴,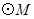 的方程为
的方程为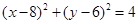 ,过
,过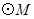 上任一点
上任一点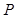 作
作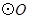 的切线
的切线 ,
,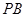 ,切点为
,切点为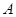 ,
, 。
。
(1)求椭圆的方程;
(2)若直线 与
与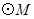 的另一交点为
的另一交点为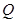 ,当弦
,当弦 最大时,求直线
最大时,求直线 的方程;
的方程;
(3)求 的最大值与最小值。
的最大值与最小值。