如图,在RtΔABC中,∠C=90°,AC=3,BC=4,P为边AC上一个点(可以包括点C但不包括点A),以P为圆心PA为半径作⊙P交AB于点D,过点D作OP的切线交边BC于点E.试猜想BE与DE的数量关系,并说明理由.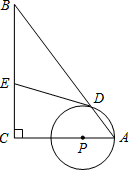
已知y-5与x成正比例,且当x=-2时,y=-1.
(1)写出y与x之间的函数关系式;
(2)当x=4时,求y的值;
如图,平行四边形ABCD(两组对边平行且相等)的边长AB=4,BC=2,若把它放在直角坐标系内,使AB在x轴上,点C在y轴上,点A的坐标是(-3,0),求点B、C、D的坐标.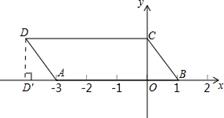
如图,在平面直角坐标系中,A(﹣2,2),B(﹣3,﹣2)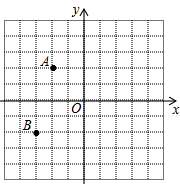
(1)若点D与点A关于y轴对称,则点D的坐标为 .
(2)将点B先向右平移5个单位再向上平移1个单位得到点C,则点C的坐标为 .
(3)求A,B,C,D组成的四边形ABCD的面积。
如图△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,△DEA 绕点A旋转,边AD、AE与BC分别与AD、AE相交于点F、G,CB=5.
回答下列问题:
(1)求证:△GAF∽△GBA;
(2)求证:AF2=FG•FC;
(3)设y=AF2+AG2,FG=x,求y与x的函数关系式;(不要求写出自变量的取值范围)
(4)探究BF2、FG2、GC2之间的关系,证明你的结论.
如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果CD=15,BE=10,sinA= ,求⊙O的半径.
,求⊙O的半径.