为了估计鱼塘中成品鱼（个体质量在0．5kg及以上，下同）的总质量，先从鱼塘中捕捞50条成品鱼，称得它们的质量如下表：
| 质量/kg |
0．5 |
0．6 |
0．7 |
1．0 |
1．2 |
1．6 |
1．9 |
| 数量/条 |
1 |
8 |
15 |
18 |
5 |
1 |
2 |
然后做上记号再放回水库中，过几天又捕捞了100条成品鱼，发现其中2条带有记号．
（1）请根据表中数据补全下面的直方图（各组中数据包括左端点不包括右端点）．
（2）根据图中数据分组，估计从鱼塘中随机捕一条成品鱼，其质量落在哪一组的可能性最大？
（3）请你用适当的方法估计鱼塘中成品鱼的总质量（精确到1kg）．
已知两个连体的正方形（有两条边在同一条直线上）在正方形网格上的位置如图所示，请你把它分割后，拼接成一个新的正方形. （要求：在正方形网格图中用实线画出拼接成的新正方形且新正方形的顶点在网格的格点上，不写作法）.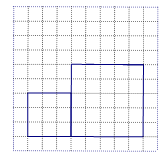
某展览大厅有3个入口和2个出口，其示意图如下. 参观者从任意一个入口进入，参观结束后从任意一个出口离开.
（1）用树状图表示，小明从进入到离开，对于入口和出口的选择有多少种不同的结果？
（2）小明从入口1进入并从出口A离开的概率是多少？
（1）解方程：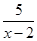
＋1＝
；
（2）解不等式组：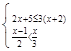
，并写出它的自然数解.
（1）计算：
－(
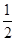)－1－
（2）先化简，再求值：
÷(x－
)，其中x＝
－1
如图，一条直线与反比例函数y1＝
的图象交于A(1，5)，B(5，n)两点，与x轴交于D点， AC⊥x轴，垂足为C．
(1)如图甲，①求反比例函数的解析式；②求n的值及D点坐标．
(2)如图乙，若点E在线段AD上运动，连结CE，作∠CEF=45°，EF交AC于F点．
①试说明△CDE∽△EAF；
②当△ECF为等腰三角形时，请求出F点的坐标．