已知平行四边形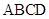 ,
, ,
,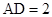 ,
,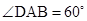 ,
, 为
为 的中点,把三角形
的中点,把三角形
沿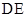 折起至
折起至 位置,使得
位置,使得 ,
,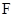 是线段
是线段 的中点.
的中点.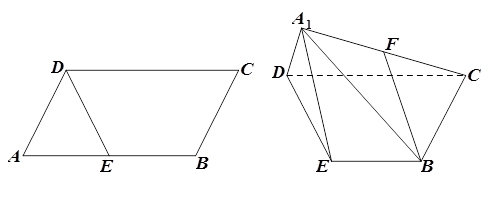
(1)求证: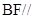 平面
平面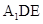 ;
;
(2)求证:平面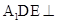 平面
平面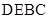 ;
;
(3)求四棱锥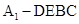 的体积.
的体积.
在平面直角坐标系
中,己知圆
在
上截得线段长为
,在
轴上截得线段长为
.
(Ⅰ)求圆心
的轨迹方程;
(Ⅱ)若
点到直线
的距离为 ,求圆
的方程.
,求圆
的方程.
经销商经销某种农产品,在一个销售季度内,每售出1
该产品获利润500元,未售出的产品,每1
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如下图所示.经销商为下一个销售季度购进了130
该农产品.以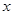 (单位:
,100≤
≤150)表示下一个销售季度内的市场需求量,
(单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:
,100≤
≤150)表示下一个销售季度内的市场需求量,
(单位:元)表示下一个销售季度内经销该农产品的利润.
(Ⅰ)将
表示为
的函数;
(Ⅱ)根据直方图估计利润
不少于57000元的概率.
如图,直三棱柱
中,
分别是
的中点.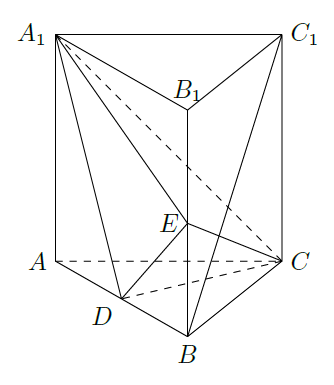
(Ⅰ)证明:
平面
;
(Ⅱ)设
,求三棱锥
的体积.
已知等差数列
的公差不为零,
,且
成等比数列.
(Ⅰ)求
的通项公式;
(Ⅱ)求
.
设
均为正数,且
,证明:
(Ⅰ)
(Ⅱ)