(本小题满分12分)如图,在四棱柱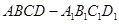 中,底面
中,底面 是等腰梯形,
是等腰梯形, ∥
∥ ,
, ,
, ,顶点
,顶点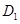 在底面
在底面 内的射影恰为点
内的射影恰为点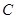 .
.
(1)求证: ;
;
(2)若直线 与直线
与直线 所成的角为
所成的角为 ,求平面
,求平面 与平面
与平面 所成角(锐角)的
所成角(锐角)的
余弦函数值.
已知点P(2,1)在抛物线C1:x2=2py(p>0)上,直线l过点Q(0,2)且与抛物线C1交于A、B两点.
(1)求抛物线C1的方程及弦AB中点M的轨迹C2的方程;
(2)若直线l1、l2分别为C1、C2的切线,且l1∥l2,求l1到l2的最近距离.
某工厂某种产品的年产量为1000x件,其中x∈[20,100],需要投入的成本为C(x),当x∈[20,80]时,C(x)=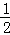 x2﹣30x+500(万元);当x∈(80,100]时,C(x)=
x2﹣30x+500(万元);当x∈(80,100]时,C(x)=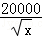 (万元).若每一件商品售价为
(万元).若每一件商品售价为 (万元),通过市场分析,该厂生产的商品能全部售完.
(万元),通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(x)(万元)关于x的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
如图,四棱锥P﹣ABCD的底面是菱形,∠ABC=60°,PA⊥底面ABCD,E,F分别是BC,PC的中点,点H在PD上,且EH⊥PD,PA=AB=2.
(1)求证:EH∥平面PBA;
(2)求三棱锥P﹣AFH的体积.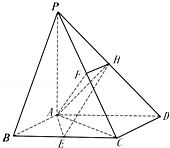
已知如图为函数f(x)=2sin(ωx+φ)(ω>0,0<φ<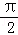 )的部分图象.
)的部分图象.
(1)求f(x)的解析式及其单调递增区间;
(2)求函数g(x)= 的值域.
的值域.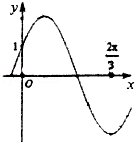
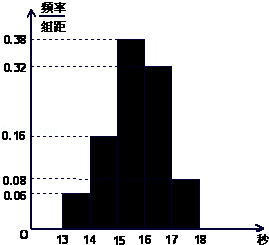
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],下图是按上述分组方法得到的频率分布直方图.
(1)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(2)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于l的概率.