(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系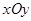 中,圆
中,圆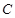 的参数方程
的参数方程 为参数).以
为参数).以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆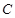 的极坐标方程;
的极坐标方程;
(Ⅱ)直线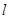 的极坐标方程是
的极坐标方程是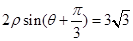 ,射线
,射线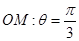 与圆
与圆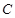 的交点为
的交点为 ,与直线
,与直线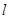 的交点为
的交点为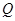 ,求线段
,求线段 的长.
的长.
(本小题满分15分)求函数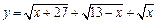 的最大和最小值.
的最大和最小值.
(本小题15分)已知 ,
, 是实数,方程
是实数,方程 有两个实根
有两个实根 ,
, ,数列
,数列 满足
满足 ,
, ,
,
(Ⅰ)求数列 的通项公式(用
的通项公式(用 ,
, 表示);
表示);
(Ⅱ)若 ,
, ,求
,求 的前
的前 项和.
项和.
(本小题满分14分)设直线 (其中
(其中 ,
, 为整数)与椭圆
为整数)与椭圆 交于不同两点
交于不同两点 ,
, ,与双曲线
,与双曲线 交于不同两点
交于不同两点 ,
, ,问是否存在直线
,问是否存在直线 ,使得向量
,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
在非负数构成的 数表
数表
中每行的数互不相同,前6列中每列的三数之和为1, ,
, ,
, ,
, ,
, ,
, ,
, 均大于.如果
均大于.如果 的前三列构成的数表
的前三列构成的数表
满足下面的性质 :对于数表
:对于数表 中的任意一列
中的任意一列 (
( ,2,…,9)均存在某个
,2,…,9)均存在某个
使得
⑶ .
.
求证:
(ⅰ)最小值 ,
, ,2,3一定自数表
,2,3一定自数表 的不同列.
的不同列.
(ⅱ)存在数表 中唯一的一列
中唯一的一列 ,
, ,2,3使得
,2,3使得 数表
数表
仍然具有性质 .
.
设 ,
, 是给定的两个正整数.证明:有无穷多个正整数
是给定的两个正整数.证明:有无穷多个正整数 ,使得
,使得 与
与 互素.
互素.