某中学将 名高一新生分成水平相同的甲、乙两个“平行班”,每班
名高一新生分成水平相同的甲、乙两个“平行班”,每班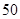 人,吴老师采用
人,吴老师采用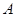 、
、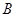 两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取
两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取 名学生的成绩进行统计,作出的茎叶图如下:
名学生的成绩进行统计,作出的茎叶图如下:
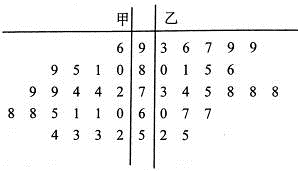
记成绩不低于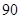 分者为“成绩优秀”.
分者为“成绩优秀”.
(1)在乙班样本的 个个体中,从不低于
个个体中,从不低于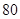 分的成绩中随机抽取
分的成绩中随机抽取 个,记随机变量
个,记随机变量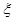 为抽到“成绩优秀”的个数,求
为抽到“成绩优秀”的个数,求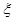 的分布列及数学期望
的分布列及数学期望 ;
;
(2)由以上统计数据填写下面 列联表,并判断有多大把握认为“成绩优秀”与教学方式有关?
列联表,并判断有多大把握认为“成绩优秀”与教学方式有关?
| |
甲班( 方式) 方式) |
乙班( 方式) 方式) |
总计 |
| 成绩优秀 |
|
|
|
| 成绩不优秀 |
|
|
|
| 总计 |
|
|
|
如图,海上有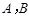 两个小岛相距10
两个小岛相距10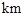 ,船O将保持观望A岛和B岛所成的视角为
,船O将保持观望A岛和B岛所成的视角为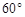 ,现从船O上派下一只小艇沿
,现从船O上派下一只小艇沿 方向驶至
方向驶至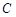 处进行作业,且
处进行作业,且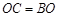 .设
.设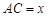
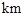 。
。
(1)若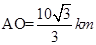 ,求出
,求出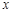 的取值;
的取值;
(2)用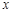 分别表示
分别表示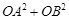 和
和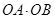 ,并求出
,并求出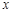 的取值范围.
的取值范围.
集合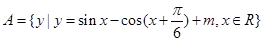 ,
,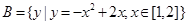 ,若命题
,若命题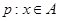 ,命题
,命题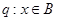 ,且
,且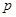 是
是 必要不充分条件,求实数
必要不充分条件,求实数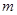 的取值范围。
的取值范围。
设函数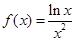 ,
,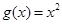 .
.
(1)求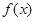 的极大值;
的极大值;
(2)求证:
(3)当方程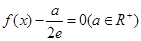 有唯一解时,试探究函数
有唯一解时,试探究函数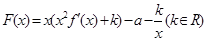 与
与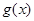 的图象在其公共点处是否存在公切线,若存在.研究
的图象在其公共点处是否存在公切线,若存在.研究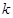 的值的个数;若不存在,请说明理由.
的值的个数;若不存在,请说明理由.
已知数列 中,
中, 且点
且点 在直线
在直线 上。
上。
(1)求数列 的通项公式;
的通项公式;
(2)若函数 求函数
求函数 的最小值;
的最小值;
(3)设 表示数列
表示数列 的前项和.试问:是否存在关于
的前项和.试问:是否存在关于 的整式
的整式 ,使得
,使得 对于一切不小于2的自然数
对于一切不小于2的自然数 恒成立?若存在,写出
恒成立?若存在,写出 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
某重点大学自主招生考试过程依次为自荐材料审查、笔试、面试共三轮考核。规定:只能通过前一轮考核才能进入下一轮的考核,否则将被淘汰;三轮考核都通过才算通过该高校的自主招生考试。学生甲三轮考试通过的概率分别为 ,
, ,
, ,且各轮考核通过与否相互独立。
,且各轮考核通过与否相互独立。
(1)求甲通过该高校自主招生考试的概率;
(2)若学生甲每通过一轮考核,则家长奖励人民币1000元作为大学学习的教育基金。记学生甲得到教育基金的金额为 ,求
,求 的分布列和数学期望。
的分布列和数学期望。