(本小题满分14分)已知函数 在
在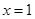 处的切线
处的切线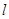 与直线
与直线 垂直,
垂直,
函数 .
.
(1)求实数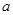 的值;
的值;
(2)若函数 存在单调递减区间,求实数
存在单调递减区间,求实数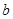 的取值范围;
的取值范围;
(3)设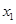 ,
,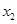 (
(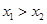 )是函数
)是函数 的两个极值点,若
的两个极值点,若 ,求
,求 的最小值.
的最小值.
已知数列 满足:
满足: ,
, ,
, ,
, .
.
(1)若 ,且数列
,且数列 为等比数列,求
为等比数列,求 的值;
的值;
(2)若 ,且
,且 为数列
为数列 的最小项,求
的最小项,求 的取值范围.
的取值范围.
如图,已知椭圆O: +y2=1的右焦点为F,点B,C分别是椭圆O的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.
+y2=1的右焦点为F,点B,C分别是椭圆O的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.
(1)当直线PM过椭圆的右焦点F时,求△FBM的面积;
(2)①记直线BM,BP的斜率分别为k1,k2,求证:k1·k2为定值;
②求 的取值范围.
的取值范围.
图1是一段半圆柱形水渠的直观图,其横断面如图2所示,其中C为半圆弧 的中点,渠宽AB为2米.
的中点,渠宽AB为2米.
(1)当渠中水深CD为0.4米时,求水面的宽度;
(2)若把这条水渠改挖(不准填土)成横断面为等腰梯形的水渠,且使渠的底面与地面平行,则当改挖后的水渠底宽为多少时,所挖出的土量最少?
如图,在直四棱柱ABCD﹣A1B1C1D1中, E,F分别是AB,BC的中点,A1C1与B1D1交于点O.
(1)求证:A1,C1,F,E四点共面;
(2)若底面ABCD是菱形,且 A1E,求证:
A1E,求证: 平面A1C1FE.
平面A1C1FE.
在 中,三个内角A,B,C所对的边分别为a,b,c,且满足
中,三个内角A,B,C所对的边分别为a,b,c,且满足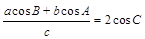 .
.
(1)求角C的大小;
(2)若 的面积为
的面积为 ,
, ,求边
,求边 的长.
的长.