如图,在梯形 中
中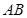 ‖
‖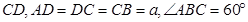 ,平面
,平面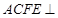 平面
平面 ,四边形
,四边形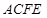 是矩形,
是矩形,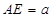 ,点
,点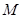 在线段
在线段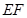 上.
上.
(Ⅰ)求证: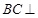 平面
平面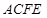 ;
;
(Ⅱ)当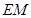 为何值时,
为何值时,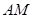 ‖平面
‖平面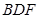 ?证明你的结论;
?证明你的结论;
(Ⅲ)求二面角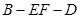 的大小.
的大小. 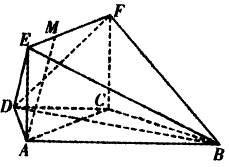
17五名学生在玩模奖游戏,游戏规则是:取5个编号为1、2、3、4、5的相同小球装入袋中,五名同学也分别编上1、2、3、4、5号,然后五人依次从袋中模一球,若某人摸到的球的编号和自己的编号相同则该同学获奖。
(1)求甲获奖的概率;
(2)设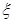 表示获奖人数,求
表示获奖人数,求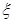 的概率分布列和数学期望。
的概率分布列和数学期望。
(1)已知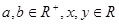 ,求证:
,求证: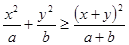 ;
;
(2)已知实数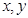 满足:
满足: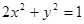 ,试利用(1)求
,试利用(1)求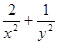 的最小值。
的最小值。
已知数列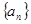 满足:
满足: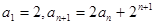 。
。
(1)若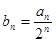 ,求证:数列
,求证:数列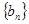 为等差数列;
为等差数列;
(2)求数列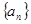 的前
的前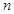 项和
项和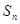
已知椭圆中心在原点,焦点在 轴上,离心率
轴上,离心率 ,过椭圆的右焦点且垂直于长轴的弦长为
,过椭圆的右焦点且垂直于长轴的弦长为
(1)求椭圆的标准方程;
(2) 为椭圆左顶点,
为椭圆左顶点,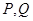 为椭圆上异于
为椭圆上异于 的任意两点,若
的任意两点,若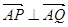 ,求证:直线
,求证:直线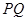 过定点并求出定点坐标。
过定点并求出定点坐标。