【改编】(本小题满分12分)已知椭圆C: 过点
过点 ,且椭圆C的离心率为
,且椭圆C的离心率为 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ) 为坐标原点,斜率为
为坐标原点,斜率为 的直线过
的直线过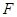 点,且与点
点,且与点 的轨迹交于点
的轨迹交于点 ,
, ,若
,若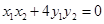 ,求△
,求△ 的面积.
的面积.
已知集合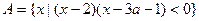 ,函数
,函数 的定义域为B。
的定义域为B。
(1)若a=2求集合B;
(2)若A=B,求实数a的值。
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点.
(1)求证: B1D^平面PQR;
B1D^平面PQR;
(2)设二面角B1-PR-Q的大小为q,求|cosq|.
一个口袋中装有大小和质地都相同的白球和红球共7个, 其中白球个数不少于红球个数.依次从口袋中任取一球,如果取到红球,那么继续取球,且取出的红球不放回;如果取到白球,就停止取球.记取球的次数为随机变量X.若P(X=2)=
其中白球个数不少于红球个数.依次从口袋中任取一球,如果取到红球,那么继续取球,且取出的红球不放回;如果取到白球,就停止取球.记取球的次数为随机变量X.若P(X=2)= .
.
(1)求口袋中的白球个数;
(2)求 X的概率分布与数学期望.
X的概率分布与数学期望.
选修4—5:不等式选讲
解不等式:∣2x-1∣+3x>1.
选修4— 4:坐标系与参数方程
4:坐标系与参数方程
在极坐标系中,已知直线l:rcos(q+)=,圆C:r=4cosq,求直线l被圆C截得的弦长.