(本小题满分15分)己知⊙O: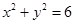 ,
,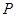 为⊙O上动点,过
为⊙O上动点,过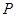 作
作 轴于
轴于 ,
,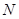 为
为 上一点,且
上一点,且 .
.
(Ⅰ)求点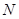 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)若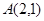 ,
, ,过
,过 的直线与曲线
的直线与曲线 相交于
相交于 、
、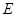 两点,则
两点,则 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
解关于 的一元二次不等式
的一元二次不等式 .
.
设椭圆的方程为 ,斜率为1的直线不经过原点
,斜率为1的直线不经过原点 ,而且与椭圆相交于
,而且与椭圆相交于 两点,
两点, 为线段
为线段 的中点.
的中点.
(1)问:直线 与
与 能否垂直?若能,
能否垂直?若能, 之间满足什么关系;若不能,说明理由;
之间满足什么关系;若不能,说明理由;
(2)已知 为
为 的中点,且
的中点,且 点在椭圆上.若
点在椭圆上.若 ,求椭圆的离心率.
,求椭圆的离心率.
在正方体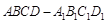 中,
中,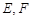 分别
分别 的中点.
的中点.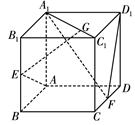
(1)求证: ;
;
(2)已知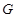 是靠近
是靠近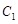 的
的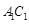 的四等分点,求证:
的四等分点,求证: .
.
已知函数 的定义域为
的定义域为 .设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.
.设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.
(1)求证: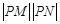 是定值;
是定值;
(2)判断并说明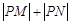 有最大值还是最小值,并求出此最大值或最小值.
有最大值还是最小值,并求出此最大值或最小值.
已知数列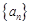 的前
的前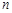 项和
项和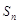 满足
满足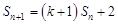 ,又
,又 ,
,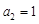 .
.
(1)求实数k的值;
(2)问数列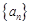 是等比数列吗?若是,给出证明;若不是,说明理由;
是等比数列吗?若是,给出证明;若不是,说明理由;
(3)求出数列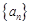 的前
的前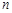 项和
项和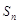 .
.