如图,抛物线 与坐标轴相交于
与坐标轴相交于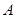 、
、 、
、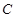 三点,
三点,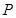 是线段
是线段 上一动点(端点除外),过
上一动点(端点除外),过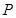 作
作 ,交
,交 于点
于点 ,连接
,连接 .
.
(1)直接写出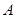 、
、 、
、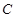 的坐标;
的坐标;
(2)求抛物线 的对称轴和顶点坐标;
的对称轴和顶点坐标;
(3)求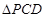 面积的最大值,并判断当
面积的最大值,并判断当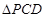 的面积取最大值时,以
的面积取最大值时,以 、
、 为邻边的平行四边形是否为菱形.
为邻边的平行四边形是否为菱形.
如图,已知A(-4,0.5),B(-1,2)是一次函数y=ax+b与反比例函数 (m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.
实施新课程改革后,学生的自主学习、合作交流能力有很大提高,张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成两幅不完整的统计图,请你根据统计图解答下列问题:
(1)本次调查中,张老师一共调查了名同学,其中C类女生有名,D类男生有名;
(2)将条形统计图补充完整;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,则所选两位同学恰好是一位男同学和一位女同学的概率是.
小明同学在解一元二次方程时,他是这样做的:
(1)小明的解法从第步开始出现错误;此题的正确结果是.
(2)用因式分解法解方程:x(2x-1)=3(2x-1)
已知双曲线y= (k>0,x>0)与矩形ABCD,A(2,1)C(6,4)设双曲线与折线A-D-C交于E,与折线A-B-C交于F.
(k>0,x>0)与矩形ABCD,A(2,1)C(6,4)设双曲线与折线A-D-C交于E,与折线A-B-C交于F.
(1)写出B,D两点的坐标;
(2)k为何值时,双曲线与矩形有公共点;
(3)设△AEF的面积为y,当E,F分别在DC和BC上时,确定y与k之间的函数关系式,并确定k取值范围;
(4)当E,F分别在DC和BC上,且△AEF为直角三角形,求k的值;
(5)直接写出EF的最大值.
小明妈妈,每天需赶头班公交车,驶往终点站.离他家最近的公交站点离终点站15km,一天他妈妈从家步行到公交站点,恰好赶上头班公交车,上车后才发现有重要物品落在家中,急忙通知小明将物品送到终点站,这时妈妈已上车5min,小明马上取了东西,用时6min赶到妈妈上车的公交站点,乘坐刚好路过的出租车,沿公交车的线路驶往公交车的终点站,结果比公交车早4min到达,出租车与小明一起等候公交车.若公交车,出租车均视为全程匀速行驶,出租车的速度为60km/h(即:1km/min).设妈妈所乘公交车离开她上车的站点的时间为t(min),小明上车后,小明所乘出租车距妈妈上车的公交站点的路程为S1(km),妈妈所乘的公交车与小明所乘出租车之间相距的路程为S(km)
(1)求S1与t之间的函数关系式,并写出t的取值范围;
(2)写出11≤t≤30,S与t之间的函数关系式;
(3)公交车到达终点之前,经多长时间两车相距500m.