已知椭圆 的左、右焦点分别是
的左、右焦点分别是 ,离心率为
,离心率为 ,过
,过 且垂直于
且垂直于 轴的直线被椭圆
轴的直线被椭圆 截得的线段长为
截得的线段长为 ;
;
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若P为椭圆C在第一象限内的任意一点,过点P且斜率为 的直线与椭圆相切,设
的直线与椭圆相切,设 的斜率分别为
的斜率分别为 ,试证明
,试证明 为定值,并求出此定值;
为定值,并求出此定值;
(Ⅲ)若直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,且原点O到直线l的距离为1,设
,且原点O到直线l的距离为1,设 ,当
,当 时,求
时,求 的面积
的面积 的取值范围.
的取值范围.
已知 ,函数
,函数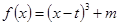 .
.
(1)当 时,若
时,若 ,求函数
,求函数 的单调区间;
的单调区间;
(2)若关于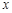 的不等式
的不等式 在区间
在区间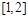 上有解,求
上有解,求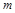 的取值范围;
的取值范围;
(3)已知曲线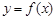 在其图象上的两点
在其图象上的两点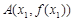 ,
,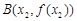 (
(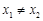 )处的切线分别为
)处的切线分别为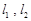 .若直线
.若直线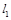 与
与 平行,试探究点
平行,试探究点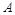 与点
与点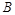 的关系,并证明你的结论.
的关系,并证明你的结论.
已知抛物线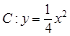 的焦点为
的焦点为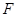 ,点
,点 为抛物线
为抛物线 上的一个动点,过点
上的一个动点,过点 且与抛物线
且与抛物线 相切的直线记为
相切的直线记为 .
.
(1)求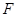 的坐标;
的坐标;
(2)当点 在何处时,点
在何处时,点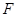 到直线
到直线 的距离最小?
的距离最小?
已知: 为常数)
为常数)
(1)若 ,求
,求 的最小正周期;
的最小正周期;
(2)若 在[
在[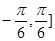 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求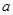 的值.
的值.
如图,在四棱锥 中,底面
中,底面 是菱形,
是菱形,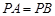 ,且侧面
,且侧面 平面
平面 ,点
,点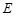 是棱
是棱 的中点.
的中点.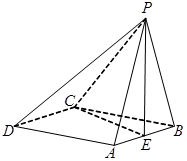
(1)求证: 平面
平面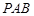 ;
;
(2)求证: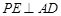 ;
;
(3)若 ,求证:平面
,求证:平面 平面
平面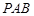 .
.
在甲、乙两个盒子中分别装有编号为1,2,3,4的四个形状相同的小球,现从甲、乙两个盒子中各取出1个小球,每个小球被取出的可能性相等.
(1)求取出的两个球上的编号都为奇数的概率;
(2)求取出的两个球上的编号之和为3的倍数的概率;
(3)求取出的两个球上的编号之和大于6的概率.