(年湖南湘西12分)湘西盛产椪柑,春节期间,一外地运销客户安排15辆汽车装运A、B、C三种不同品质的椪柑120吨到外地销售,按计划15辆汽车都要装满且每辆汽车只能装同一种品质的椪柑,每种椪柑所用车辆部不少于3辆.
(1)设装运A种椪柑的车辆数为x辆,装运B种椪柑车辆数为y辆,根据下表提供的信息,求出y与x之间的函数关系式;
| 椪柑品种 |
A |
B |
C |
| 每辆汽车运载量 |
10 |
8 |
6 |
| 每吨椪柑获利(元) |
800 |
1200 |
1000 |
(2)在(1)条件下,求出该函数自变量x的取值范围,车辆的安排方案共有几种?请写出每种安排方案;
(3)为了减少椪柑积压,湘西州制定出台了促进椪柑销售的优惠政策,在外地运销客户原有获利不变的情况下,政府对外地运销客户,按每吨50元的标准实行运费补贴.若要使该外地运销客户所获利润W(元)最大,应采用哪种车辆安排方案?并求出利润W(元)的最大值?
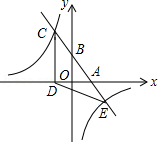
如图,一次函数 、 为常数, 的图象与 轴、 轴分别交于 、 两点,且与反比例函数 为常数,且 的图象在第二象限交于点 . 轴,垂足为 ,若 .
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为 ,求 的面积;
(3)直接写出不等式 的解集.
如图,在 的方格纸中, 的三个顶点都在格点上.
(1)在图1中,画出一个与 成中心对称的格点三角形;
(2)在图2中,画出一个与 成轴对称且与 有公共边的格点三角形;
(3)在图3中,画出
绕着点
按顺时针方向旋转
后的三角形.
如图1,抛物线 与 轴交于 , 两点,过点 的直线 分别与 轴及抛物线交于点 , .
(1)求直线和抛物线的表达式;
(2)动点 从点 出发,在 轴的负半轴上以每秒1个单位长度的速度向左匀速运动,设运动时间为 秒,当 为何值时, 为直角三角形?请直接写出所有满足条件的 的值;
(3)如图2,将直线 沿 轴向下平移4个单位后,与 轴, 轴分别交于 , 两点,在抛物线的对称轴上是否存在点 ,在直线 上是否存在点 ,使 的值最小?若存在,求出其最小值及点 , 的坐标;若不存在,请说明理由.

【问题解决】
一节数学课上,老师提出了这样一个问题:如图1,点 是正方形 内一点, , , .你能求出 的度数吗?
小明通过观察、分析、思考,形成了如下思路:
思路一:将 绕点 逆时针旋转 ,得到△ ,连接 ,求出 的度数;
思路二:将 绕点 顺时针旋转 ,得到△ ,连接 ,求出 的度数.
请参考小明的思路,任选一种写出完整的解答过程.
【类比探究】
如图2,若点 是正方形 外一点, , , ,求 的度数.

如图,已知 , 分别为 的边 , 上两点,点 , , 在 上,点 , 在 上. 为 上一点,连接 并延长交 的延长线于点 ,交 于点 .
(1)若 为 ,请将 用含 的代数式表示;
(2)若 ,请说明当 为多少度时,直线 为 的切线;
(3)在(2)的条件下,若 ,求 的值.
