(年贵州贵阳12分)如图,经过点A(0,﹣6)的抛物线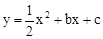 与x轴相交于B(﹣2,0),C两点.
与x轴相交于B(﹣2,0),C两点.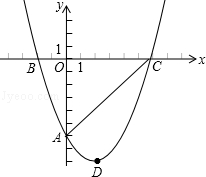
(1)求此抛物线的函数关系式和顶点D的坐标;
(2)将(1)中求得的抛物线向左平移1个单位长度,再向上平移m(m>0)个单位长度得到新抛物线y1,若新抛物线y1的顶点P在△ABC内,求m的取值范围;
(3)在(2)的结论下,新抛物线y1上是否存在点Q,使得△QAB是以AB为底边的等腰三角形?请分析所有可能出现的情况,并直接写出相对应的m的取值范围.
一辆货车从超市出发,向东走了3千米到达小彬家,继续向东走了1.5千米到达小颖家,然后向西走了9.5千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,请你在数轴上表示出小明家,小彬家和小颖家的位置.
(2)小明家距小彬家多远?
(3)如果货车耗油量是每千米0.02升,那么在上述过程中共耗油多少升?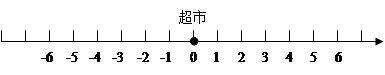
先化简,后求值:
(1)先化简,后求值: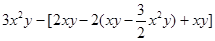 ,其中
,其中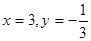
(2)求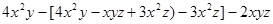 的值,其中负数
的值,其中负数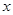 的绝对值是2,正数
的绝对值是2,正数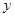 的倒数是它的本身,负数
的倒数是它的本身,负数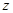 的平方等于9;
的平方等于9;
如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,c满足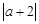 +(c-8)2=0.
+(c-8)2=0.
(1)a = ,b = ,c = .
(2)若将数轴折叠,使得A点与B点重合,则点C与数 表示的点重合.
(3)点A,B,C开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和点C分别以每秒4个单位长度和8个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB = ,AC = ,BC = .(用含t的代数式表示)
(4)请问:3AB-(2BC+AC)的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
图①、图②分别由两个长方形拼成.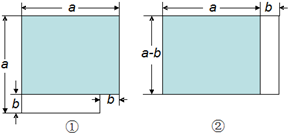
(1)观察思考:
(Ⅰ)图①的两个长方形的面积和S1= ;
A.a2+b2 B.a2+ab C.b2-ab D.a2-b2
(Ⅱ)图②的两个长方形的面积和S2= ;
A.a(a-b) B.b(a-b) C.(a+b)(a-b) D.ab(a+b)
(2)过程探索:
| a的取值 |
b的取值 |
S1 |
S2 |
| a=5 |
b=2 |
||
| a=7.5 |
b=4.5 |
猜想归纳:S1 S2(填“>”或“=”或“<”)
结论应用:10000.52-9999.52(写出具体计算过程)
某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下.(单位:km)
| 第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
第六次 |
第七次 |
| -4 |
+7 |
-9 |
+10 |
+6 |
-5 |
-6 |
(1)求收工时,检修小组在A地的哪个方向?距离A地多远?
(2)在第几次记录时距A地最近?
(3)若汽车行驶每千米耗油0.2升,问从A地出发,检修结束后再回到A地共耗油多少升?