如图：在数轴上A点表示数a，B点示数b，C点表示数c，b是最-优题课

如图：在数轴上A点表示数a，B点示数b，C点表示数c，b是最小的正整数，且a，c满足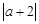+（c－8）²=0．

（1）a =       ，b =       ，c =       ．
（2）若将数轴折叠，使得A点与B点重合，则点C与数       表示的点重合．
（3）点A，B，C开始在数轴上运动，若点A以每秒2个单位长度的速度向左运动，同时，点B和点C分别以每秒4个单位长度和8个单位长度的速度向右运动，假设t秒钟过后，若点A与点B之间的距离表示为AB，点A与点C之间的距离表示为AC，点B与点C之间的距离表示为BC．则AB =       ，AC =       ，BC =       ．（用含t的代数式表示）
（4）请问：3AB－（2BC+AC）的值是否随着时间t的变化而改变? 若变化，请说明理由；若不变，请求其值．

科目数学题型解答题难度中等

知识点：数轴

已知直线 $y = \frac{1}{2} x + 2$ 分别交 $x$ 轴、 $y$ 轴于 $A$ 、 $B$ 两点，抛物线 $y = \frac{1}{2} x^{2} + mx - 2$ 经过点 $A$ ，和 $x$ 轴的另一个交点为 $C$ ．

（1）求抛物线的解析式；

（2）如图1，点 $D$ 是抛物线上的动点，且在第三象限，求 $ΔABD$ 面积的最大值；

（3）如图2，经过点 $M (- 4, 1)$ 的直线交抛物线于点 $P$ 、 $Q$ ，连接 $CP$ 、 $CQ$ 分别交 $y$ 轴于点 $E$ 、 $F$ ，求 $OE \cdot OF$ 的值．

备注：抛物线顶点坐标公式 $(- \frac{b}{2 a}$ ， $\frac{4 ac - b^{2}}{4 a})$

如图，在矩形 $ABCD$ 中， $AD = 5$ ， $CD = 4$ ，点 $E$ 是 $BC$ 边上的点， $BE = 3$ ，连接 $AE$ ， $DF ⊥ AE$ 交于点 $F$ ．

（1）求证： $ΔABE ≅ ΔDFA$ ；

（2）连接 $CF$ ，求 $\sin ∠ DCF$ 的值；

（3）连接 $AC$ 交 $DF$ 于点 $G$ ，求 $\frac{AG}{GC}$ 的值．

端午节期间，甲、乙两人沿同一路线行驶，各自开车同时去离家560千米的景区游玩，甲先以每小时60千米的速度匀速行驶1小时，再以每小时 $m$ 千米的速度匀速行驶，途中休息了一段时间后，仍按照每小时 $m$ 千米的速度匀速行驶，两人同时到达目的地，图中折线、线段分别表示甲、乙两人所走的路程 $y_{甲} (km)$ ， $y_{乙} (km)$ 与时间 $x (h)$ 之间的函数关系的图象．请根据图象提供的信息，解决下列问题：

（1）图中 $E$ 点的坐标是　，题中 $m =$ 　　 $km / h$ ，甲在途中休息　　 $h$ ；

（2）求线段 $CD$ 的解析式，并写出自变量 $x$ 的取值范围；

（3）两人第二次相遇后，又经过多长时间两人相距 $20 km$ ？

如图， $AB$ 是 $⊙ O$ 的直径， $AC$ 为弦， $∠ BA$ 的平分线交 $⊙ O$ 于点 $D$ ，过点 $D$ 的切线交 $AC$ 的延长线于点 $E$ ．

求证：（1） $DE ⊥ AE$ ；

（2） $AE + CE = AB$ ．

已知关于 $x$ 的一元二次方程 $x^{2} - 5 x + 2 m = 0$ 有实数根．

（1）求 $m$ 的取值范围；

（2）当 $m = \frac{5}{2}$ 时，方程的两根分别是矩形的长和宽，求该矩形外接圆的直径．