(年江苏盐城12分)如图①,在平面直角坐标系中,一块等腰直角三角板ABC的直角顶点A在y轴上,坐标为(0,﹣1),另一顶点B坐标为(﹣2,0),已知二次函数 的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y轴且经过点B,直尺沿x轴正方向平移,当A′D′与y轴重合时运动停止.
的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y轴且经过点B,直尺沿x轴正方向平移,当A′D′与y轴重合时运动停止.
(1)求点C的坐标及二次函数的关系式;
(2)若运动过程中直尺的边A′D′交边BC于点M,交抛物线于点N,求线段MN长度的最大值;
(3)如图②,设点P为直尺的边A′D′上的任一点,连接PA、PB、PC,Q为BC的中点,试探究:在直尺平移的过程中,当 时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
(说明:点与抛物线的位置关系可分为三类,例如,图②中,点A在抛物线内,点C在抛物线上,点D′在抛物线外.)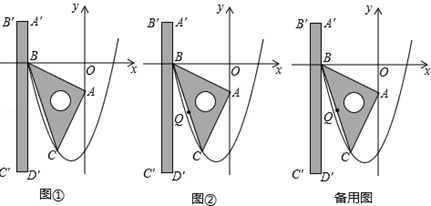
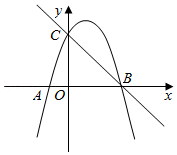
如图,已知二次函数 的图象经过点 , ,与 轴交于点 .
(1)求抛物线的解析式;
(2)抛物线上是否存在点 ,使 ,若存在请直接写出点 的坐标.若不存在,请说明理由.
如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中, 的三个顶点 、 、 均在格点上.
(1)将 向左平移5个单位得到△ ,并写出点 的坐标;
(2)画出△ 绕点 顺时针旋转 后得到的△ ,并写出点 的坐标;
(3)在(2)的条件下,求△ 在旋转过程中扫过的面积(结果保留 .

先化简,再求值: ,其中 .
如图,已知直线 与 轴交于点 ,与 轴交于点 ,线段 的长是方程 的一个根, .请答案下列问题:
(1)求点 , 的坐标;
(2)直线 交 轴负半轴于点 ,交 轴正半轴于点 ,交直线 于点 .若 是 的中点, ,反比例函数 图象的一支经过点 ,求 的值;
(3)在(2)的条件下,过点 作 ,垂足为 ,点 在直线 上,点 在直线 上.坐标平面内是否存在点 ,使以 , , , 为顶点的四边形是正方形?若存在,请写出点 的个数,并直接写出其中两个点 的坐标;若不存在,请说明理由.

某商场准备购进 , 两种书包,每个 种书包比 种书包的进价少20元,用700元购进 种书包的个数是用450元购进 种书包个数的2倍, 种书包每个标价是90元, 种书包每个标价是130元.请答案下列问题:
(1) , 两种书包每个进价各是多少元?
(2)若该商场购进 种书包的个数比 种书包的2倍还多5个,且 种书包不少于18个,购进 , 两种书包的总费用不超过5450元,则该商场有哪几种进货方案?
(3)该商场按(2)中获利最大的方案购进书包,在销售前,拿出5个书包赠送给某希望小学,剩余的书包全部售出,其中两种书包共有4个样品,每种样品都打五折,商场仍获利1370元.请直接写出赠送的书包和样品中, 种书包各有几个?