（年广东汕尾10分）如图，已知抛物线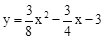
与x轴的交点为A、D（A在D的右侧），与y轴的交点为C．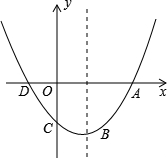
（1）直接写出A、D、C三点的坐标；
（2）若点M在抛物线上，使得△MAD的面积与△CAD的面积相等，求点M的坐标；
（3）设点C关于抛物线对称轴的对称点为B，在抛物线上是否存在点P，使得以A、B、C、P四点为顶点的四边形为梯形？若存在，请求出点P的坐标；若不存在，请说明理由．
我们知道，平方差公式是： (a+b)(a-b) = a2 - b2，反过来得到：a2 - b2=(a+b)(a-b)也成立，在解决某些问题时逆用平方差公式会起到很好的效果，如：计算：
根据平方差逆用方法，请计算下列各题：
(1) 
；(2分)
(2) 正整数m、n满足m2- n2=7，求m、n的值.(3分)
如图，已知AB∥CD,∠A=100°，CB平分∠ACD,求∠3的度数.
有一张明星演唱会的门票，小明和小亮都想获得这张门票，亲自体验明星演唱会的热烈气氛，小红为他们出了一个主意，方法就是：从印有1、2、3、4、5、4、6、7的8张扑克牌中任取一张，抽到比4大的牌，小明去；否则，小亮去．
（1）求小明抽到4的概率；
（2）你认为这种方法对小明和小亮公平吗？请说明理由；若不公平，请你修改游戏规则，使游戏对双方都公平．
已知：如图，DG⊥BC AC⊥BC，EF⊥AB，∠1=∠2.求证：EF∥CD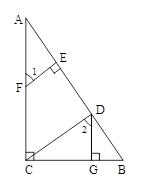
证明：∵ DG⊥BC,AC⊥BC( )
∴ ∠DGB=∠ACB=90º(垂直的定义)
∴ DG∥AC （ ）
∴ ∠2 = ( )
∵ ∠1=∠2 ( )
∴ ∠1=∠DCA(等量代换)
∴ EF∥CD ( )
先化简，再求值：
÷
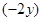，其中，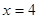
,
.