(年辽宁本溪14分)如图,直线y=x﹣4与x轴、y轴分别交于A、B两点,抛物线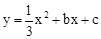 经过A、B两点,与x轴的另一个交点为C,连接BC.
经过A、B两点,与x轴的另一个交点为C,连接BC.
(1)求抛物线的解析式及点C的坐标;
(2)点M在抛物线上,连接MB,当∠MBA+∠CBO=45°时,求点M的坐标;
(3)点P从点C出发,沿线段CA由C向A运动,同时点Q从点B出发,沿线段BC由B向C运动,P、Q的运动速度都是每秒1个单位长度,当Q点到达C点时,P、Q同时停止运动,试问在坐标平面内是否存在点D,使P、Q运动过程中的某一时刻,以C、D、P、Q为顶点的四边形为菱形?若存在,直接写出点D的坐标;若不存在,说明理由.
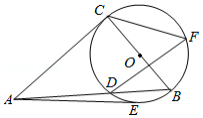
如图, 中, ,以 为直径的 交 于点 , 、 是 上两点,连接 、 、 ,满足 .
(1)求证: 是 的切线;
(2)若 的半径为3, ,求 的长.
今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到 港口正西方的 处时,发现在 的北偏东 方向,相距150海里处的 点有一可疑船只正沿 方向行驶, 点在 港口的北偏东 方向上,海监船向 港口发出指令,执法船立即从 港口沿 方向驶出,在 处成功拦截可疑船只,此时 点与 点的距离为 海里.
(1)求 点到直线 的距离;
(2)执法船从 到 航行了多少海里?(结果保留根号)
近年来雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注.某单位计划在室内安装空气净化装置,需购进 、 两种设备.每台 种设备价格比每台 种设备价格多0.7万元,花3万元购买 种设备和花7.2万元购买 种设备的数量相同.
(1)求 种、 种设备每台各多少万元?
(2)根据单位实际情况,需购进 、 两种设备共20台,总费用不高于15万元,求 种设备至少要购买多少台?
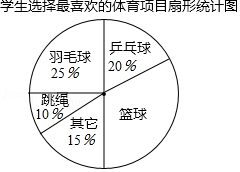
某校以“我最喜爱的体育项目”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项),根据调查数据绘制了如下不完整的统计表和扇形统计图:
学生选择最喜爱的体育项目统计表
|
运动项目 |
频数(人数) |
频率 |
|
篮球 |
36 |
0.30 |
|
羽毛球 |
|
0.25 |
|
乒乓球 |
24 |
|
|
跳绳 |
12 |
0.10 |
|
其它项目 |
18 |
0.15 |
请根据以上图表信息解答下列问题:
(1)统计表中的 , ;
(2)在扇形统计图中,“篮球”所在扇形的圆心角为 度;
(3)该学校共有2400名学生,据此估计有多少名学生最喜爱乒乓球?
(4)将2名最喜爱篮球的学生和2名最喜爱羽毛球的学生编为一组,从中随机抽取两人,请用列表或画树状图的方法求出所抽取的两人都选择了最喜爱篮球的概率.
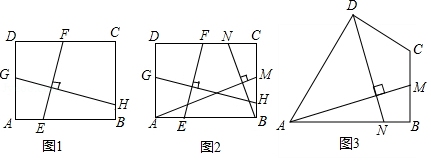
(探究证明)
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
如图1,矩形 中, , 分别交 , 于点 , , 分别交 , 于点 , .求证: ;
(结论应用)
(2)如图2,在满足(1)的条件下,又 ,点 , 分别在边 , 上,若 ,则 的值为 ;
(联系拓展)
(3)如图3,四边形 中, , , , ,点 , 分别在边 , 上,求 的值.