已知AB是⊙O的直径，AB=4，点C在线段AB的延长线上运动，点D在⊙O 上运动（不与点B重合），连接CD，且CD=OA.
（1）当OC=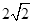
时（如图），求证：CD是⊙O的切线；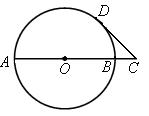
（2）当OC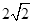＞时，CD所在直线于⊙O相交，设另一交点为E，连接AE.
①当D为CE中点时，求△ACE的周长;
②连接OD，是否存在四边形AODE为梯形？若存在，请说明梯形个数并求此时AE·ED的值；若不存在，请说明理由。
某水果批发市场经销一种水果，如果每千克盈利10元，每天可售出500千克．经市场调查发现，在进货价不变的情况下，若每千克这种水果在原售价的基础上每涨价1元，日销售量将减少20千克．如果市场某天销售这种水果盈利了6 000元，同时顾客又得到了实惠，那么每千克这种水果涨了多少元?
设每千克这种水果涨价x元时(0＜x≤25)，市场每天销售这种水果所获利润为y元．若不考虑其它因素，单纯从经济角度看，每千克这种水果涨价多少元时，市场每天销售这种水果盈利最多?最多盈利多少元?
已知：如图，等腰△ABC中，AB＝BC，AE⊥BC于E，EF⊥AB于F，若CE＝2，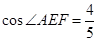
，求EF的长．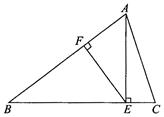
已知抛物线y＝ax2＋bx＋c经过点A(0，3)、B(4，3)、C(1，0)．填空：抛物线的对称轴为直线x＝______，抛物线与x轴的另一个交点D的坐标为______；
求该抛物线的解析式．
已知：如图，∠MAN＝45°，B为AM上的一个定点．若点P在射线AN上，以P为圆心，PA为半径的圆与射AN的另一个交点为C．请确定⊙P的位置，使BC恰与⊙P相切．
画出⊙P；(不要求尺规作图，不要求写画法)
连结BC、BP并填空：
①∠ABC＝______°；
②比较大小：∠ABP______∠CBP．(用“＞”、“＜”或“＝”连接)
已知：如图，△ABC中，AB＝2，BC＝4，D为BC边上一点，BD＝1．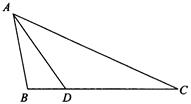
求证：△ABD∽△CBA；
若DE∥AB交AC于点E，请再写出另一个与△ABD相似的三角形，并直接写出DE的长．