如图，某中学甲、乙两班共有25名学生报名参加了一项 测试．这25位学生的考分编成的茎叶图，其中有一个数据因电脑操作员不小心删掉了（这里暂用x来表示），但他清楚地记得两班学生成绩的中位数相同．
（Ⅰ）求这两个班学生成绩的中位数及x的值；
（Ⅱ）如果将这些成绩分为“优秀”（得分在175分 以上，包括175分）和“过关”，若学校再从这两个班获得“优秀”成绩的考生中选出3名代表学校参加比赛，求这3人中甲班至多有一人入选的概率．
（本小题满分12分）已知椭圆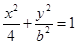
（0＜b＜2）的离心率等于
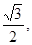抛物线
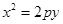（p＞0）.
（1）若抛物线的焦点F在椭圆的顶点上，求椭圆和抛物线的方程；
（II）若抛物
线的焦点F为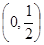
，在抛物线上是否存在点P，使得过点P的切线与椭圆相交于A，B两点，且满足
？若存在，求出点P的坐标；若不存在，请说明理由.
（本小题满分12分）现有正整数1，2，3，4，5，…n，一质点从第一个数1出发顺次跳动，质点的跳动步数通过抛掷骰子来决定：骰子的点数小于等于4时，质点向前跳一步；骰子的
点数大于
4时，质点向前跳两步.
（I）若抛掷骰子二次，
质点到达的正整数记为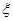
，求E；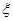
（II）求质点恰好到达正整数5的概率.
（本小题满分12分）如图三棱柱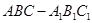
中，底面
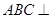侧面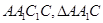
为等边三角形，
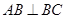且AB=BC，三棱锥
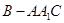的体积为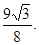
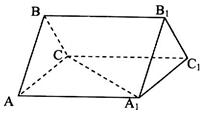
（I）求证：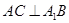
；
（II）求直线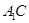
与平面BAA1所成角的正弦值.
（本小题满分12分）设
是单调递增的等差数列，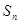
为其前n项和，且满足
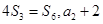是
的等比中项.
（I）求数列的通项公式；
（II）是否存在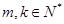
，使
？说明理由；
（III）若数列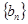
满足
求数列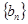的通项公式.
（本小题满分12分）
已知向量
且满足
（I）求函数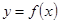
的单调递增区间；
（II）设
的内角A满足
且
，求边BC的最小值.