如图,在菱形 中,
中,
 沿对角线
沿对角线 将△
将△ 折起,使
折起,使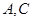 之间的距离为
之间的距离为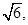 若
若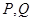 分别为线段
分别为线段 上的动点
上的动点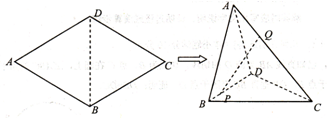
(1)求线段 长度的最小值;
长度的最小值;
(2)当线段 长度最小时,求直线
长度最小时,求直线 与平面
与平面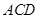 所成角的正弦值
所成角的正弦值
已知数列 中,
中,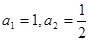 且数列
且数列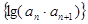 的前n项和
的前n项和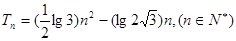 又设
又设 。
。
(Ⅰ)求证:数列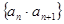 是等比数列;
是等比数列;
(II)求数列 的通项
的通项 及前n项和
及前n项和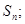
(III)求证: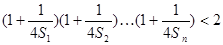
已知在直角坐标平面XOY中,有一个不在Y轴上的动点P(x,y),到定点F(0, )的距离比它到X轴的距离多
)的距离比它到X轴的距离多 ,记P点的轨迹为曲线C
,记P点的轨迹为曲线C
(I)求曲线C的方程;
(II)已知点M在Y轴上,且过点F的直线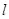 与曲线C交于A、B两点,若
与曲线C交于A、B两点,若  为正三角形,求M点的坐标与直线
为正三角形,求M点的坐标与直线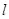 的方程。
的方程。
设函数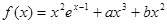 ,已知
,已知 和
和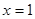 为
为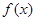 的极值点。
的极值点。
(I)求a和b的值;
(II)设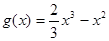 ,试证
,试证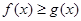 恒成立。
恒成立。
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”.
(I)从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为  ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(II)根据频率分布直方图填写下面 列联表,并判断是否有95%的把握认为“成绩优秀”与教学方式有关。
列联表,并判断是否有95%的把握认为“成绩优秀”与教学方式有关。
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,CE∥AB。
(Ⅰ)求证:CE⊥平面PAD;
(Ⅱ)若PA=AB=1,AD=3,且CD与平面PAD所成的角为45°,求二面角B—PE—A的正切值。