(本题4分)
对于任何实数,我们规定符号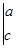
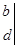 =
=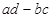 ,例如:
,例如: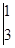
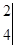 =
=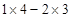 =
=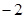
(1)按照这个规律请你计算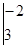
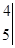 的值;
的值;
(2)按照这个规定请你计算,当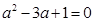 时,
时,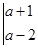
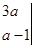 的值.
的值.
有一张边长为 厘米的正方形桌面,因为实际需要,需将正方形边长增加 厘米,木工师傅设计了如图所示的三种方案:

小明发现这三种方案都能验证公式: ,
对于方案一,小明是这样验证的:
请你根据方案二、方案三,写出公式的验证过程.
方案二:
方案三:
如图,在 中, 是对角线, , ,垂足分别为点 , ,求证: .

如图1,直线 与 轴交于点 ,与 轴交于点 ,点 是线段 上一动点 .以点 为圆心, 长为半径作 交 轴于另一点 ,交线段 于点 ,连接 并延长交 于点 .
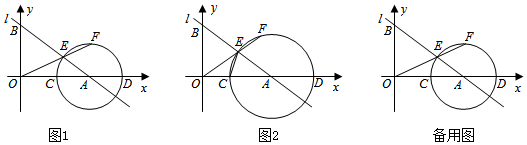
(1)求直线 的函数表达式和 的值;
(2)如图2,连接 ,当 时,
①求证: ;
②求点 的坐标;
(3)当点 在线段 上运动时,求 的最大值.
若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.
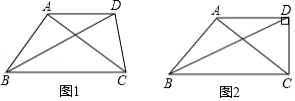
(1)已知 是比例三角形, , ,请直接写出所有满足条件的 的长;
(2)如图1,在四边形 中, ,对角线 平分 , .求证: 是比例三角形.
(3)如图2,在(2)的条件下,当 时,求 的值.
某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元.已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
(1)求甲、乙两种商品的每件进价;
(2)该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变.要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?