已知抛物线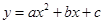 (
( )经过A(
)经过A( ,0),B(2,0)两点,与y轴相交于点C,点D为该抛物线的顶点.
,0),B(2,0)两点,与y轴相交于点C,点D为该抛物线的顶点.
(1)求该抛物线的解析式及点D的坐标;
(2)点E是该抛物线上一动点,且位于第一象限,当点E到直线BC的距离为 时,求点E的坐标;
时,求点E的坐标;
(3)在(2)的条件下,在x轴上有一点P,且∠EAO+∠EPO=∠α,当tanα=2时,求点P的坐标.
在我们学习过的数学教科书中,有一个数学活动,若身旁没有量角器或三角尺,又需要作 , , 等大小的角,可以采用如下方法:
操作感知:
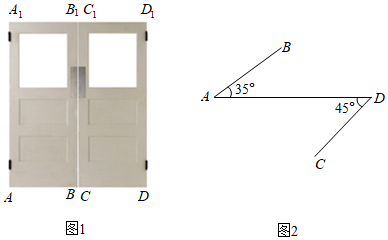
第一步:对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展开(如图1 .
第二步:再一次折叠纸片,使点 落在 上,并使折痕经过点 ,得到折痕 ,同时得到线段 (如图 .
猜想论证:
(1)若延长 交 于点 ,如图3所示,试判定 的形状,并证明你的结论.
拓展探究:
(2)在图3中,若 , ,当 , 满足什么关系时,才能在矩形纸片 中剪出符合(1)中结论的三角形纸片 ?

为了倡导“节约用水,从我做起”,某市政府决定对该市直属机关200户家庭用水情况进行调查.市政府调查小组随机抽查了其中部分家庭一年的月平均用水量(单位:吨),调查中发现,每户家庭月平均用水量在 吨范围内,并将调查结果制成了如下尚不完整的统计表:
|
月平均用水量(吨 |
3 |
4 |
5 |
6 |
7 |
|
频数(户数) |
4 |
|
9 |
10 |
7 |
|
频率 |
0.08 |
0.40 |
|
|
0.14 |
请根据统计表中提供的信息解答下列问题:
(1)填空: , , .
(2)这些家庭中月平均用水量数据的平均数是 ,众数是 ,中位数是 .
(3)根据样本数据,估计该市直属机关200户家庭中月平均用水量不超过5吨的约有多少户?
(4)市政府决定从月平均用水量最省的甲、乙、丙、丁四户家庭中,选取两户进行“节水”经验分享.请用列表或画树状图的方法,求出恰好选到甲、丙两户的概率,并列出所有等可能的结果.
如图1是某中学教学楼的推拉门,已知门的宽度 米,且两扇门的大小相同(即 ,将左边的门 绕门轴 向里面旋转 ,将右边的门 绕门轴 向外面旋转 ,其示意图如图2,求此时 与 之间的距离(结果保留一位小数).(参考数据: , ,
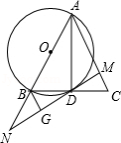
如图,在 中, 是 边上的中线,以 为直径的 交 于点 ,过 作 于点 ,交 的延长线于点 ,过点 作 于 .
(1)求证: ;
(2)求证:直线 是 的切线.
如图, 是 的对角线.
(1)尺规作图(请用 铅笔):作线段 的垂直平分线 ,交 , , 分别于 , , ,连接 , (保留作图痕迹,不写作法).
(2)试判断四边形 的形状并说明理由.
