(本小题满分12分)
已知椭圆 经过点
经过点 ,离心率为
,离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)不垂直与坐标轴的直线 与椭圆
与椭圆 交于
交于 两点, 以
两点, 以 为直径的圆过原点,且线段
为直径的圆过原点,且线段 的垂直平分线交y轴于点
的垂直平分线交y轴于点 ,求直线
,求直线 的方程。
的方程。
已知函数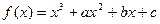 的图象过原点,且
的图象过原点,且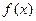 在
在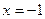 、
、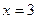 处取得极值.
处取得极值.
(Ⅰ)求函数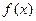 的单调区间及极值;
的单调区间及极值;
(Ⅱ)若函数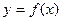 与
与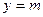 的图象有且仅有一个公共点,求实数
的图象有且仅有一个公共点,求实数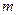 的取值范围.
的取值范围.
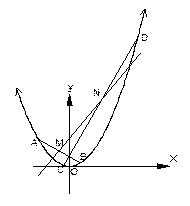
(本小题满分12分)已知抛物线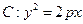 的准线方程
的准线方程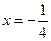 ,
,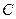 与直线
与直线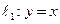 在第一象限相交于点
在第一象限相交于点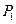 ,过
,过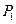 作
作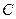 的切线
的切线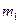 ,过
,过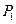 作
作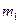 的垂线
的垂线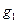 交x轴正半轴于点
交x轴正半轴于点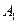 ,过
,过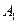 作
作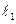 的平行线
的平行线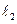 交抛物线
交抛物线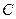 于第一象限内的点
于第一象限内的点 ,过
,过 作抛物线
作抛物线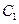 的切线
的切线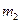 ,过
,过 作
作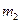 的垂线
的垂线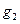 交x轴正半轴于点
交x轴正半轴于点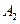 ,…,依此类推,在x轴上形成一点列
,…,依此类推,在x轴上形成一点列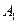 ,
,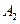 ,
, ,…,
,…,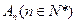 ,设点
,设点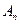 的坐标为
的坐标为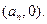
(Ⅰ)试探求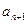 关于
关于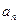 的递推关系式;
的递推关系式;
(Ⅱ)求证: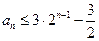 ;
;
(Ⅲ)求证: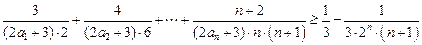 .
.
(本小题满分12分)设圆 过点P(0,2), 且在
过点P(0,2), 且在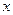 轴上截得的弦RG的长为4.
轴上截得的弦RG的长为4.
(Ⅰ)求圆心 的轨迹E的方程;
的轨迹E的方程;
(Ⅱ)过点 (0,1),作轨迹
(0,1),作轨迹 的两条互相垂直的弦
的两条互相垂直的弦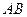 ,
,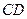 ,设
,设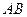 、
、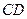 的中点分别为
的中点分别为 ,
,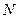 ,试判断直线
,试判断直线 是否过定点?并说明理由.
是否过定点?并说明理由.
(本小题满分12分)某工厂生产某种儿童玩具,每件玩具的成本为30元,并且每件玩具的加工费为 元(其中
元(其中 为常数,且
为常数,且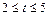 ),设该工厂每件玩具的出厂价为
),设该工厂每件玩具的出厂价为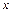 元(
元(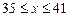 ),根据市场调查,日销售量与
),根据市场调查,日销售量与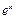 (
(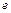 为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.
为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.
(Ⅰ)求该工厂的日利润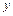 (元)与每件玩具的出厂价
(元)与每件玩具的出厂价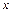 元的函数关系式;
元的函数关系式;
(Ⅱ)当每件玩具的日售价为多少元时,该工厂的利润 最大,并求
最大,并求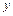 的最大值.
的最大值.
(本小题满分13分)一个袋中有大小相同的标有1,2,3,4,5,6的6个小球,某人做如下游戏,每次从袋中拿一个球(拿后放回),记下标号.若拿出球的标号是3的倍数,则得1分,否则得 分.
分.
(Ⅰ)求拿4次至少得2分的概率;
(Ⅱ)求拿4次所得分数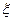 的分布列和数学期望.
的分布列和数学期望.