阅读材料:
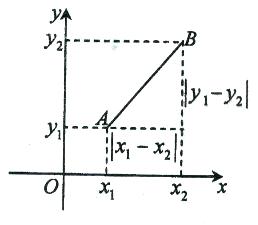
如图,在平面直角坐标系中,O为坐标原点,对于任意两点A (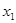 ,
,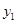 ),
),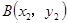 ,由勾股定理可得:
,由勾股定理可得: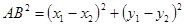 ,我们把
,我们把 叫做A、B两点之间的距离,记作
叫做A、B两点之间的距离,记作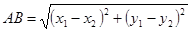 .
.
例题:在平面直角坐标系中,O为坐标原点,设点P(x,0).
A(0,2),B (3,-2),则AB= .;PA = .;
解:由定义有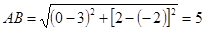 ;
;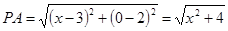 .
.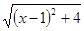 表示的几何意义是 .;
表示的几何意义是 .;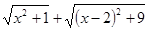 表示的几何意义是 ..
表示的几何意义是 ..
解:因为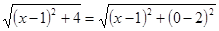 ,所以
,所以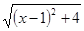 表示的几何意义是点
表示的几何意义是点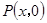 到点
到点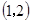 的距
的距
离;同理可得,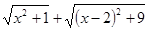 表示的几何意义是点
表示的几何意义是点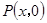 分别到点(0,1)和点(2,3)的距离和.
分别到点(0,1)和点(2,3)的距离和.
根据以上阅读材料,解决下列问题:
(1)如图,已知直线 与反比例函数
与反比例函数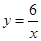 (
(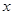 >0)的图像交于
>0)的图像交于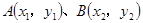 两点,
两点,
则点A、B的坐标分别为A( , ),B( , ),AB= .
(2)在(1)的条件下,设点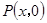 ,则
,则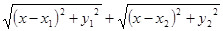 表示的几何意义
表示的几何意义
是 ;试求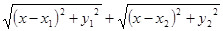 的最小值,以及取得最小值时点P的坐标.
的最小值,以及取得最小值时点P的坐标.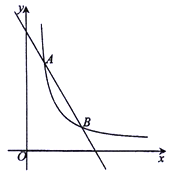
如图,经过平移,△ABC的顶点A移到了点D,请作出平移后的三角形。
因式分解:(4分×4=16分)
(1) (2)9x2+12xy+4y2;(3)
(2)9x2+12xy+4y2;(3) 
(4)
计算与解方程组:(4分×6=24分)
(1)
(2) 
(3) 
(4) 
(5) 
(6) 
宽与长的比是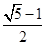 的矩形叫黄金矩形.心理测试表明:黄金矩形令人赏心悦目,它给我们以协调,匀称的美感.现将小波同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图所示):
的矩形叫黄金矩形.心理测试表明:黄金矩形令人赏心悦目,它给我们以协调,匀称的美感.现将小波同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图所示):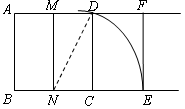
第一步:作一个正方形ABCD;
第二步:分别取AD,BC的中点M,N,连接MN;
第三步:以N为圆心,ND长为半径画弧,交BC的延长线于E;
第四步:过E作EF⊥AD,交AD的延长线于F.
请你根据以上作法,证明矩形DCEF为黄金矩形.
在数学学习过程中,通常是利用已有的知识与经验,通过对研究对象进行观察、实验、推理、抽象概括,发现数学规律,揭示研究对象的本质特征。
比如“同底数幂的乘法法则”的学习过程是利用有理数的乘方概念和乘法结合律,由“特殊”到“一般”进行抽象概括的: 22×23=25,23×24=27,22×26=28,…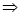
2m×2n=2m+n,…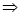 am×an=am+n(m、n都是正整数)。探索问题:
am×an=am+n(m、n都是正整数)。探索问题:
(1)比较下列各组数据的大小:
①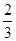
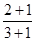 ,②
,②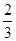
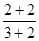 ,③
,③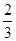
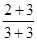 ,④
,④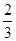
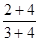 ,…。
,…。
(2)请你根据上面的材料归纳出a、b、c(a>b>0,c>0)之间的一个数学关系式;并用已学的数学知识说明你发现结论的正确性.
(3)试用(2)中你归纳的数学关系式,解释下面生活中的一个现象:“若m克糖水里含有n克糖,再加入k克糖(仍不饱和),则糖水更甜了”;