如图,长方体中,,点分别在上,.过点的平面与此长方体的面相交,交线围成一个正方形.

(Ⅰ)在图中画出这个正方形(不必说出画法和理由);
(Ⅱ)求直线与平面所成角的正弦值.
设函数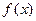 的定义域为
的定义域为 ,当
,当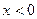 时,
时, ,且对任意的实数
,且对任意的实数 ,有
,有 .
.
⑴求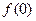 ,判断并证明函数
,判断并证明函数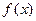 的单调性;
的单调性;
⑵数列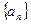 满足
满足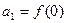 ,且
,且
①求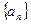 通项公式;
通项公式;
②当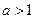 时,不等式
时,不等式 对不小于
对不小于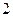 的正整数恒成立,求
的正整数恒成立,求 的取值范围.
的取值范围.
已知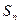 为数列
为数列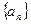 的前
的前 项和,
项和, ,
,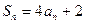 .
.
⑴设数列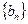 中,
中, ,求证:
,求证: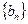 是等比数列;
是等比数列;
⑵设数列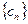 中,
中,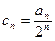 ,求证:
,求证: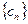 是等差数列;
是等差数列;
⑶求数列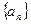 的通项公式及前
的通项公式及前 项和.
项和.
【解题思路】由于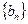 和
和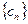 中的项与
中的项与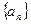 中的项有关,且
中的项有关,且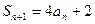 ,可利用
,可利用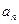 、
、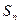 的关系作为切入点.
的关系作为切入点.
已知等差数列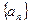 与等比数列
与等比数列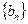 中,
中,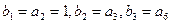 ,求
,求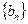 的通项.
的通项.
观察下面由奇数组成的数阵,回答下列问题: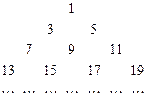
⑴求第六行的第一个数;
⑵求第20行的第一个数;
⑶求第20行的所有数的和.
首项为正数的数列
满足
.
(Ⅰ)证明:若
为奇数,则对一切
,
都是奇数;
(Ⅱ)若对一切
,都有
,求
的取值范围。