△ABC中D是BC上的点,AD平分∠BAC,BD2DC.（Ⅰ-优题课

$△ A B C$ 中 $D$ 是 $B C$ 上的点, $A D$ 平分 $∠ B A C, B D = 2 D C$ .

（Ⅰ）求 $\frac{\sin ∠ B}{\sin ∠ C}$ ；
（Ⅱ）若 $∠ B A C = 60^{°}$ ,求 $∠ B$ .

科目数学题型解答题难度中等

已知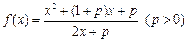
（1）若p > 1时，解关于x的不等式；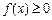
（2）若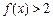对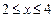时恒成立，求p的范围．

数列{a_n}中a₁ = 2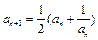，，{b_n}中．
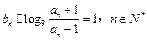（1）求证：数列{b_n}为等比数列，并求出其通项公式；
（2）当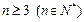时，证明：．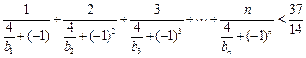

已知点A(– 2，0)，B(2，0)，动点P满足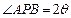：，且.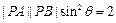
（1）求动点P的轨迹G的方程；
（2）过点B的直线l与轨迹G交于两点M、N．试问在x轴上是否存在定点C，使得为常数.若存在，求出点C的坐标；若不存在，说明理由．

已知圆C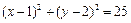：，直线l：．
（1）证明：不论m取什么实数时，直线l与圆恒交于两点；
（2）求直线l被圆C截得的线段的最短长度以及此时直线l的方程．

数列{a_n}中，a₁ = 1，当时，其前n项和满足
（1）求S_n的表达式；
（2）设，数列{b_n}的前n项和为T_n，求T_n．