已知函数 .
(Ⅰ)当
时,求不等式
的解集;
(Ⅱ)若
的图像与
轴围成的三角形面积大于6,求
的取值范围.
如图所示,空间四边形ABCD中,E、F、G分别在AB、BC、CD上,且满足AE∶EB=CF∶FB=2∶1,CG∶GD="" 
3∶1,过E、F、G的平面交AD于H,连接EH.
(1)求AH∶HD;
(2)求证:EH、FG、BD三线共点.
如图所示,在四棱锥P—ABCD中,底面是边长为2的菱形,∠DAB=60°,
对角线AC与BD交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为60°.
(1)求四棱锥的体积;
(2)若E是PB的中点,求异面直线DE与PA所成角的余弦值.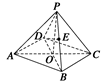
对某电子元件进行寿命追踪调查,情况如下.
| 寿命(h) |
100—200 |
200—300 |
300—400 |
400—500 |
500—600 |
| 个数 |
20 |
30 |
80 |
40 |
30 |
(1)列出频率分布表;
(2)画出频率分布直方图;
(3)估计电子元件寿命在100—400 h以内的在总体中占的比例;
(4)估计电子元件寿命在400 h以上的在总体中占的比例.
三棱锥S—ABC中,一条棱长为a,其余棱长均为1,求a为何值时VS—ABC最大,并求最大值.
如图所示,在长方体ABCD—A1B1C1D1中,AB=BC=1,BB1=2,
E是棱CC1上的点,且CE= CC1.
CC1.
(1)求三棱锥C—BED的体积;
(2)求证:A1C⊥平面BDE.