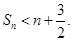在数列 中,
(1)若
求数列
的通项公式;
(2)若
证明:
已知定义在区间(0,+∞)上的函数f(x)满足f( +f(x2)=f(x1),且当x>1时,f(x)<0.
+f(x2)=f(x1),且当x>1时,f(x)<0.
(1)求f(1)的值;
(2)判断f(x)的单调性并加以证明;
(3)若f(3)=-1,解不等式f(|x|)>-2.
(本小题满分12分)、已知函数 (
( ,
, )为偶函数,且函数
)为偶函数,且函数 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)将函数 的图象向右平移
的图象向右平移 个单位后,得到函数
个单位后,得到函数 的图象,求
的图象,求 的单调递减区间.
的单调递减区间.
(本小题满分12分)
若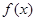 为二次函数,-1和3是方程
为二次函数,-1和3是方程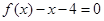 的两根,
的两根,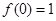
(1)求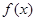 的解析式;
的解析式;
(2)若在区间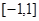 上,不等式
上,不等式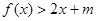 有解,求实数m的取值范围。
有解,求实数m的取值范围。
(本小题满分12分)
已知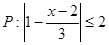 ,
, 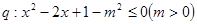 ,而非P是非q的必要条件,但不是充分条件,求实数m的取值范围。
,而非P是非q的必要条件,但不是充分条件,求实数m的取值范围。
(12分)设函数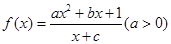 为奇函数,且
为奇函数,且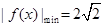 ,数列
,数列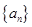 与
与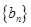 满足如下关系:
满足如下关系: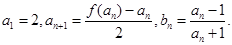
(1)求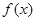 的解析式;
的解析式;
(2)求数列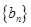 的通项公式
的通项公式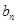 ;
;
(3)记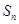 为数列
为数列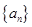 的前
的前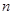 项和,求证:对任意的
项和,求证:对任意的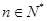 有
有