(本题满分13分)
设椭圆E:  (
( )过M(2,2e),N(2e,
)过M(2,2e),N(2e, )两点,其中e为椭圆的离心率,
)两点,其中e为椭圆的离心率, 为坐标原点.
为坐标原点.
(I)求椭圆E的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且 ?若存在,写出该圆的方程;若不存在,说明理由.
?若存在,写出该圆的方程;若不存在,说明理由.
设函数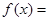 2|x-3|+|x-4|.
2|x-3|+|x-4|.
(1)求不等式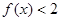 的解集;
的解集;
(2)若不等式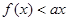 的解集不是空集,求实数a的取值范围.
的解集不是空集,求实数a的取值范围.
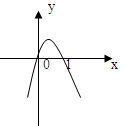
已知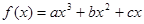 的导函数
的导函数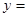
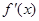 的简图,它与
的简图,它与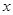 轴的交点是(0,0)和(1,0),
轴的交点是(0,0)和(1,0),
又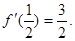
(1)求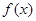 的解析式及
的解析式及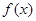 的极大值.
的极大值.
(2)若在区间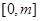 (m>0)上恒有
(m>0)上恒有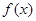 ≤x成立,求m的取值范围.
≤x成立,求m的取值范围.
已知双曲线C: 离心率是
离心率是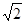 ,过点
,过点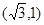 ,且右支上的弦
,且右支上的弦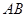 过右焦点
过右焦点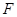 .
.
(1)求双曲线C的方程;
(2)求弦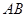 的中点
的中点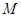 的轨迹E的方程;
的轨迹E的方程;
(3)是否存在以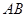 为直径的圆过原点O?,若存在,求出直线
为直径的圆过原点O?,若存在,求出直线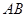 的斜率k 的值.若不存在,则说明理由.
的斜率k 的值.若不存在,则说明理由.
已知函数
 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点 处的切线的斜率是
处的切线的斜率是 .
.
(1)求实数 的值;
的值;
(2)求 在区间
在区间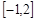 上的最大值;
上的最大值;
(3)对任意给定的正实数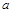 ,曲线
,曲线 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在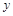 轴上?说明理由.
轴上?说明理由.
已知椭圆
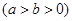 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线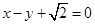 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)若过点 (2,0)的直线与椭圆
(2,0)的直线与椭圆 相交于两点
相交于两点 ,设
,设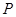 为椭圆上一点,且满足
为椭圆上一点,且满足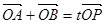 (
( 为坐标原点),当
为坐标原点),当 <
< 时,求实数
时,求实数 取值范围.
取值范围.