(本小题满分12分)
为了普及环保知识,增强环保意识,某校从理科甲班抽取60人,从文科乙班抽取50人参加环保知识测试.
(Ⅰ)根据题目条件完成下面2×2列联表,并据此判断是否有99%的把握认为环保知识成绩优秀与学生的文理分类有关.
| |
优秀人数 |
非优秀人数 |
总计 |
| 甲班 |
|
|
|
| 乙班 |
|
30 |
|
| 总计 |
60 |
|
|
(Ⅱ)现已知 三人获得优秀的概率分别为
三人获得优秀的概率分别为 ,设随机变量
,设随机变量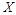 表示
表示 三人中获得优秀的人数,求
三人中获得优秀的人数,求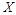 的分布列及期望
的分布列及期望 .附:
.附: ,
,
 |
0.100 |
0.050 |
0.025 |
0.010 |
0.005 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
已知函数f(x)=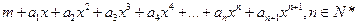 。
。
(I)若f(x)=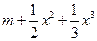 。
。
①求曲线y=f(x)上的点P(1,f(1))为切点的切线的斜率;
②若函数f(x)在x=x1处取得极大值,在x=x2处取得极小值,且点(x1,f(x1))在第二象限,点(x2,f(x2))位于y轴负半轴上,求m的取值范围;
(II)当an=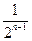 时,设函数f(x)的导函数为
时,设函数f(x)的导函数为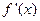 ,令Tn=
,令Tn=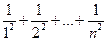 ,证明:Tn
,证明:Tn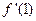 1
1
设数列{an}的首项为a1=1,前n项和为Sn,且Sn+1= 。
。
(I)求数列{an}的通项公式an;
(II)设数列{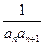 }的前n项和为Tn,是否存在最大正整数,使得对[1,+1]内的任意n
}的前n项和为Tn,是否存在最大正整数,使得对[1,+1]内的任意n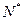 ,不等式n<
,不等式n< 恒成立?若存在,求出的值;若不存在,请说明理由。
恒成立?若存在,求出的值;若不存在,请说明理由。
已知函数f(x)=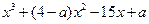 ,aR。
,aR。
(I)若点P(0,2)在函数f(x)的图象上,求a的值和函数f(x)的极小值;
(II)若函数f(x)在(1,1)上是单调递减函数,求a的最大值
第十一届西博会于2010年10月22日至26日在蓉举行,本届西博会以“绿色改变生活,技术引领发展”为主题。如此重要的国际盛会,自然少不了志愿者这支重要力量,“志愿者,西博会最亮丽的风景线”,通过他们的努力和付出,已把志愿者服务精神的种子播撒到人们心中。某大学对参加了本次西博会的该校志愿者实施“社会教育实践”学分考核,因该批志愿者表现良好,该大学决定考核只有合格和优秀两个等次,若某志愿者考核为合格,授予0.5个学分;考核为优秀,授予1个学分。假设该校志愿者甲、乙、丙考核为优秀的概率分别为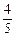 、
、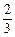 、
、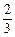 ,他们考核所得的等次相互独立。
,他们考核所得的等次相互独立。
(I)求在这次考核中,志愿者甲、乙、两三人中至少有一名考核为优秀的概率;
(II)求在这次考核中甲、乙、丙三名志愿者所得学分之和为整数的概率。
把正方形ABCD沿其对角线AC折成二面角DACB后,连结BD,得到如图所示的几何体,已知点O、E、F分别为线段AC、AD、BC的中点。
(I)求证:AB//平面EOF;
(II)求二面角EOFB的大小。