在抽样方法中,有放回抽样与无放回抽样中个体被抽到的概率是不同的,但当总体的容量很大而抽取的样本容量很小时,无放回抽样可以近似看作有放回抽样。现有一大批产品,采用随机抽样的方法一件一件抽取进行检验。若抽查的4件产品中未发现不合格产品,则停止检查,并认为该批产品合格;若在查到第4件或在此之前发现不合格产品,则也停止检查,并认为该批产品不合格。假定该批产品的不合格率为0.1,设检查产品的件数为X。
(Ⅰ)求随机变量X的分布列和数学期望;
(Ⅱ)通过上述随机抽样的方法进行质量检查,求认为该批产品不合格的概率
已知椭圆 的焦点在
的焦点在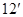 轴上,离心率为
轴上,离心率为 ,对称轴为坐标轴,且经过点
,对称轴为坐标轴,且经过点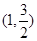 .
.
(1)求椭圆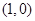 的方程;
的方程;
(2)直线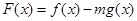 与椭圆
与椭圆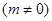 相交于
相交于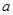 、
、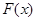 两点,
两点,  为原点,在
为原点,在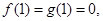 、
、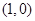 上分别存在异于
上分别存在异于 点的点
点的点 、
、 ,使得
,使得 在以
在以 为直径的圆外,求直线斜率
为直径的圆外,求直线斜率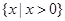 的取值范围.
的取值范围.
如图,在边长为1的等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将 沿AF折起,得到如图所示的三棱锥
沿AF折起,得到如图所示的三棱锥 ,其中
,其中 .
.

(1) 证明: //平面
//平面 ;
;
(2) 证明:
 平面
平面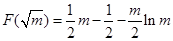 ;
;
(3)当 时,求三棱锥
时,求三棱锥 的体积
的体积
某班主任对全班50名学生进行了作业量多少的调查.数据如下表:
| 认为作业多 |
认为作业不多 |
合计 |
|
| 喜欢玩游戏 |
18 |
9 |
|
| 不喜欢玩游戏 |
8 |
15 |
|
| 合计 |
(1)请完善上表中所缺的有关数据;
(2)试通过计算说明在犯错误的概率不超过多少的前提下认为喜欢玩游戏与作业量的多少有关系?
附:
| P(K2≥K0) |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| K0 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |

已知数列 是公差不为0的等差数列,
是公差不为0的等差数列,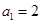 ,且
,且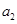 ,
, ,
,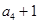 成等比数列.
成等比数列.
(1)求数列{an}的通项公式;
(2)设 ,求数列
,求数列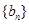 的前
的前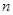 项和
项和 。
。
设向量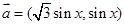 ,
,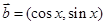 ,
,
(1)若 ,求
,求 的值;
的值;
(2)设函数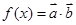 ,求
,求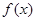 的最大值。
的最大值。