已知四棱锥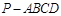
中，底面ABCD为
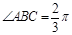的菱形，
平面ABCD，点Q在直线PA上．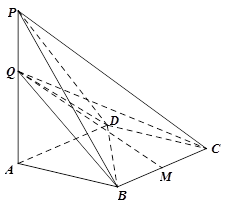
（Ⅰ）证明：直线QC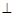
直线BD；
（Ⅱ）若二面角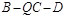
的大小为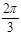
，点M为BC的中点，求直线QM与AB所成角的余弦值．
如图,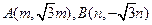 
两点分别在射线OS,OT上移动,
且
,O为坐标原点,动点P满足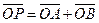
.
(1)求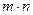
的值
(2)求点P的轨迹C的方程,并说明它表示怎样的曲线.
数列｛an｝满足a1=1,a2=2,an+2=(1+cos2
)an+sin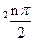
,n=1、2、3…
（1）求a3、a4并求数列｛an｝的通项公式
（2）设bn=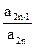
,令 Sn=
求 Sn
已知△ABC中角A、B、C所对边分别是a、b、c，设向量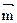
=（a，b）,
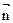=（sinB,sinA）,
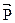=（b-2,a-2）
（1）若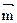//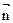，求证：△ABC为等腰三角形
（2）若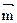⊥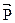，边长c="2" ，∠C=
，求△ABC的面积
某化工厂引进一条先进生产线生产某种化工产品，其生产的总成本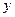
（万元）与年产量
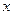（吨）之间的函数关系式可以近似地表示为
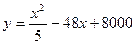，已知此生产线年产量最大为210吨。
（1）求年产量为多少吨时，生产每吨产品的平均成本最低，并求最低成本；
（2）若每吨产品平均出厂价为40万元，那么当年产量为多少吨时，可以获得最大利润？最大利润是多少？
设复数
满足
,且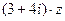
是纯虚数,求
.