抛物线 :
: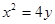 ,直线
,直线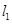 :
: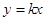 交
交 于点
于点 ,交准线于点
,交准线于点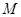 .过点
.过点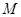 的直线
的直线 与抛物线
与抛物线 有唯一的公共点
有唯一的公共点 (
( ,
, 在对称轴的两侧),且与
在对称轴的两侧),且与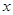 轴交于点
轴交于点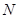 .
.
(Ⅰ)求抛物线 的准线方程;
的准线方程;
(Ⅱ)求 的取值范围.
的取值范围.
在△ABC中,三个内角A、B、C的对应边为 ,
, .
.
(Ⅰ)当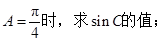
(Ⅱ)设 ,求
,求 的最大值.
的最大值.
设 函数.
函数.
(Ⅰ)求函数 单调递增区间;
单调递增区间;
(Ⅱ)当 时,求函数
时,求函数 的最大值和最小值.
的最大值和最小值.
已知数列 的前项和为
的前项和为 ,且满足
,且满足 ;
;
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 ,且
,且 的前n项和为
的前n项和为 ,求使得
,求使得 对
对 都成立的所有正整数k的值.
都成立的所有正整数k的值.
如图,在四棱锥P-ABCD中,底面为直角梯形, 垂直于底面ABCD,PA=AD=AB=2BC=2,M,N分别为PC,PB的中点.
垂直于底面ABCD,PA=AD=AB=2BC=2,M,N分别为PC,PB的中点.
(Ⅰ)求证:PB⊥DM;
(Ⅱ)求点B到平面PAC的距离.
对某校高一年级学生参加社区服务次数进行统计,随机抽取了M名学生作为样本,得到这M名学生参加社区服务的次数,根据数据作出了频数的统计如下:
| 分组 |
频数 |
频率 |
| [10,15) |
9 |
0.45 |
| [15,20) |
5 |
n |
| [20,25) |
m |
r |
| [25,30) |
2 |
0.1 |
| 合计 |
M |
1 |
(Ⅰ)求出表中M,r,m,n的值;
(Ⅱ)在所取样本中,从参加社区服务次数不少于20次的学生中任选2人,求至少有1人参加社区服务次数在区间[25,30)内的概率.