(本小题满分13分)已知函数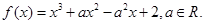
(1)当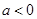 时,求函数
时,求函数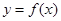 的单调区间;
的单调区间;
(2)当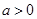 时,如果对于任意
时,如果对于任意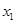 、
、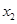 、
、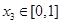 ,
,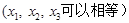 ,总存在以
,总存在以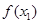 、
、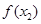 、
、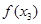 为三边长的三角形,试求实数
为三边长的三角形,试求实数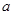 的取值范围.
的取值范围.
某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=2百米,BC=1百米.
(1)现在准备养一批供游客观赏的鱼,分别在AB、BC、CA上取点D,E,F,如图(1),使得EF‖AB,EF⊥ED,在△DEF喂食,求△DEF面积S△DEF的最大值;
(2)现在准备新建造一个荷塘,分别在AB,BC,CA上取点D,E,F,如图(2),建造△DEF连廊(不考虑宽度)供游客休憩,且使△DEF为正三角形,求△DEF边长的最小值.
如图长方体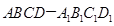 中,底面
中,底面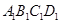 是正方形,
是正方形, 是
是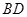 的中点,
的中点,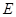 是棱
是棱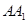 上任意一点.
上任意一点.
⑴求证: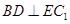 ;
;
⑵如果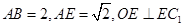 ,求
,求 的长.
的长.
设向量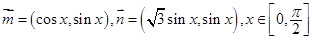 .
.
⑴若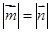 ,求
,求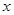 的值;
的值;
⑵设函数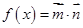 ,求
,求 的最大值.
的最大值.
已知函数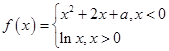 ,其中
,其中 是实数,设
是实数,设 为该函数的图象上的两点,且
为该函数的图象上的两点,且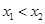 .
.
⑴指出函数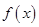 的单调区间;
的单调区间;
⑵若函数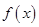 的图象在点
的图象在点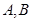 处的切线互相垂直,且
处的切线互相垂直,且 ,求
,求 的最小值;
的最小值;
⑶若函数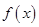 的图象在点
的图象在点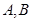 处的切线重合,求
处的切线重合,求 的取值范围.
的取值范围.
已知各项均为正数的数列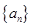 的前
的前 项和为
项和为 ,数列
,数列 的前
的前 项和为
项和为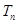 ,且
,且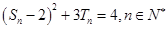 .
.
⑴证明:数列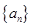 是等比数列,并写出通项公式;
是等比数列,并写出通项公式;
⑵若 对
对 恒成立,求
恒成立,求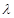 的最小值;
的最小值;
⑶若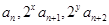 成等差数列,求正整数
成等差数列,求正整数 的值.
的值.