给定椭圆 >
> >0
>0 ,称圆心在原点
,称圆心在原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 的“伴随圆”.若椭圆
的“伴随圆”.若椭圆 的一个焦点为
的一个焦点为 ,其短轴上的一个端点到
,其短轴上的一个端点到 的距离为
的距离为
 .
.
(1)求椭圆 的方程及其“伴随圆”方程;
的方程及其“伴随圆”方程;
(2)若倾斜角为 的直线
的直线 与椭圆C只有一个公共点,且与椭圆
与椭圆C只有一个公共点,且与椭圆 的“伴随圆”相交于M、N两点,求弦MN的长;
的“伴随圆”相交于M、N两点,求弦MN的长;
(3)点 是椭圆
是椭圆 的“伴随圆”上的一个动点,过点
的“伴随圆”上的一个动点,过点 作直线
作直线 ,使得
,使得 与椭圆
与椭圆 都只有一个公共点,求证:
都只有一个公共点,求证: ⊥
⊥ .
.
已知定义在R上的函数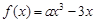 ,
,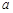 为常数,且
为常数,且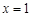 是函数
是函数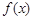 的一个极值点.
的一个极值点.
(Ⅰ)求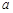 的值;
的值;
(Ⅱ)若函数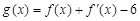 ,
,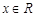 ,求
,求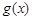 的单调区间;
的单调区间;
(Ⅲ) 过点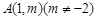 可作曲线
可作曲线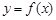 的三条切线,求
的三条切线,求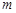 的
的 取值范围
取值范围
调查某初中1000名学生的肥胖情况,得下表:
| 偏瘦 |
正常 |
肥胖 |
|
| 女生(人) |
100 |
173 |
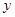 |
| 男生(人) |
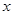 |
177 |
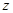 |
已知从这批学生中随机抽取1名学生,抽到偏瘦男生的概率为0.15。
(1)求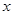 的值;
的值;
(2)若用分层抽样的方法,从这批学生中随机抽取50名,问应在肥胖学生中抽多少名?
(3)已知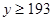 ,
,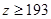 ,肥胖学生中男生不少于女生的概率。
,肥胖学生中男生不少于女生的概率。
数列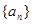 的前
的前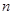 项和记为
项和记为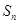 ,
,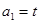 ,点
,点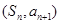 在直线
在直线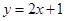 上,
上,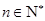 .
.
(Ⅰ)当实数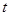 为何值时,数列
为何值时,数列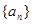 是等比数列?
是等比数列?
(Ⅱ)在(Ⅰ)的结论下,设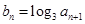 ,
,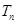 是数列
是数列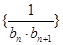 的前
的前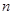 项和,求
项和,求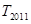 的值.
的值.
已知函数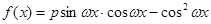
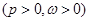 的最大值为
的最大值为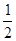 ,小正周期为
,小正周期为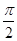 .
.
(Ⅰ)求: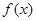 的解析式;
的解析式;
(Ⅱ)若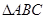 的三条边为
的三条边为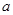 ,
,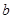 ,
,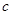 ,满足
,满足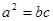 ,
,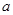 边所对的角为
边所对的角为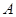 .求角
.求角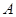 的取值范围及函数
的取值范围及函数 的值域.
的值域.