如图，矩形OABC的两边在坐标轴上，连接AC，抛物线yx24-优题课

如图，矩形O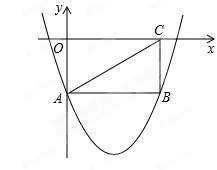ABC的两边在坐标轴上，连接AC，抛物线y=x²-4x-2经过A，B两点．

（1）求A点坐标及线段AB的长；
（2）若点P由点A出发以每秒1个单位的速度沿AB边向点B移动，1秒后点Q也由点A出发以每秒7个单位的速度沿A-O-C-B的方向向点B移动，当其中一个点到达终点时另一个点也停止移动，点P的移动时间为t秒．
①当PQ⊥AC时，求t的值；
②当PQ∥AC时，对于抛物线对称轴上一点H，当点H的纵坐标满足条件_________时，∠HOQ＜∠POQ．（直接写出答案）

科目数学题型解答题难度较难

知识点：二次函数在给定区间上的最值

随着农业技术的现代化，节水型灌溉得到逐步推广．喷灌和滴灌是比漫灌更节水的灌溉方式，喷灌和滴灌时每亩用水量分别是漫灌时的 $30 %$ 和 $20 %$ ．去年，新丰收公司用各100亩的三块试验田分别采用喷灌、滴灌和漫灌的灌溉方式，共用水15000吨．

（1）请问用漫灌方式每亩用水多少吨？去年每块试验田各用水多少吨？

（2）今年该公司加大对农业灌溉的投入，喷灌和滴灌试验田的面积都增加了 $m %$ ，漫灌试验田的面积减少了 $2 m %$ ．同时，该公司通过维修灌溉输水管道，使得三种灌溉方式下的每亩用水量都进一步减少了 $m %$ ．经测算，今年的灌溉用水量比去年减少 $\frac{9}{5} m %$ ，求 $m$ 的值．

（3）节水不仅为了环保，也与经济收益有关系．今年，该公司全部试验田在灌溉输水管道维修方面每亩投入30元，在新增的喷灌、滴灌试验田添加设备所投入经费为每亩100元，在（2）的情况下，若每吨水费为2.5元，请判断，相比去年因用水量减少所节省的水费是否大于今年的以上两项投入之和？

如图，在菱形 $ABCD$ 中， $O$ 是对角线 $BD$ 上一点 $(BO > DO)$ ， $OE ⊥ AB$ ，垂足为 $E$ ，以 $OE$ 为半径的 $⊙ O$ 分别交 $DC$ 于点 $H$ ，交 $EO$ 的延长线于点 $F$ ， $EF$ 与 $DC$ 交于点 $G$ ．

（1）求证： $BC$ 是 $⊙ O$ 的切线；

（2）若 $G$ 是 $OF$ 的中点， $OG = 2$ ， $DG = 1$ ．

①求 $\hat{HE}$ 的长；

②求 $AD$ 的长．

甲超市在端午节这天进行苹果优惠促销活动，苹果的标价为10元 $/ kg$ ，如果一次购买 $4 kg$ 以上的苹果，超过 $4 kg$ 的部分按标价6折售卖．

$x$ （单位： $kg)$ 表示购买苹果的重量， $y$ （单位：元）表示付款金额．

（1）文文购买 $3 kg$ 苹果需付款　　元；购买 $5 kg$ 苹果需付款　　元；

（2）求付款金额 $y$ 关于购买苹果的重量 $x$ 的函数解析式；

（3）当天，隔壁的乙超市也在进行苹果优惠促销活动，同样的苹果的标价也为10元 $/ kg$ ，且全部按标价的8折售卖，文文如果要购买 $10 kg$ 苹果，请问她在哪个超市购买更划算？

国家规定“中小学生每天在校体育活动时间不低于 $1 h$ ”．为此，某市就“每天在校体育活动时间”的问题随机调查了辖区内部分初中学生，根据调查结果绘制成的统计图（部分）如图所示，其中分组情况是：

$A$ 组： $t < 0.5 h$

$B$ 组： $0.5 h ⩽ t < 1 h$

$C$ 组： $1 h ⩽ t < 1.5 h$

$D$ 组： $t ⩾ 1.5 h$

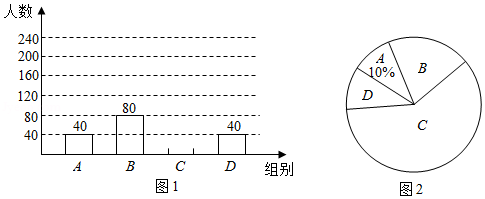
请根据上述信息解答下列问题：

（1）本次调查的人数是　　人；

（2）请根据题中的信息补全频数分布直方图；

（3） $D$ 组对应扇形的圆心角为　　 $°$ ；

（4）本次调查数据的中位数落在　　组内；

（5）若该市辖区约有80000名初中学生，请估计其中达到国家规定体育活动时间的学生人数约有多少．

如图，在 $ΔABC$ 中， $∠ B = 40 °$ ， $∠ C = 50 °$ ．

（1）通过观察尺规作图的痕迹，可以发现直线 $DF$ 是线段 $AB$ 的　　，射线 $AE$ 是 $∠ DAC$ 的　　；

（2）在（1）所作的图中，求 $∠ DAE$ 的度数．