(本小题满分12分)在边长为60 cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少?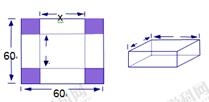
设函数
(Ⅰ)当 时,求
时,求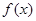 的值域;
的值域;
(Ⅱ)已知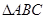 中,角
中,角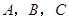 的对边分别为
的对边分别为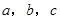 ,若
,若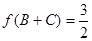 ,
,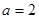 ,求
,求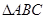 面积的最大值.
面积的最大值.
(本小题满分12分)已知函数 有如下性质:如果常数
有如下性质:如果常数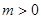 ,那么该函数在
,那么该函数在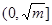 上是减函数,在
上是减函数,在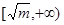 上是增函数。
上是增函数。
(Ⅰ)如果函数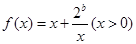 在
在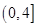 上是减函数,在
上是减函数,在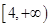 上是增函数,求实数
上是增函数,求实数 的值;
的值;
(Ⅱ)求函数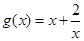 在
在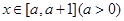 上的最小值;
上的最小值;
(Ⅲ)设常数 ,求函数
,求函数 的最大值.
的最大值.
(本小题满分12分)不等式 的解集为
的解集为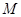 ,求函数
,求函数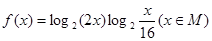 的值域.
的值域.
(本小题满分12分)已知函数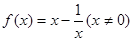
(Ⅰ)判断函数 的奇偶性;
的奇偶性;
(Ⅱ)求证:函数 在
在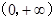 为单调增函数;
为单调增函数;
(Ⅲ)求满足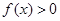 的
的 的取值范围.
的取值范围.
(本小题满分12分)某商品在近 天内每件的销售价格
天内每件的销售价格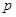 (元)与时间
(元)与时间 (天)的函数关系是
(天)的函数关系是 该商品的日销售量
该商品的日销售量 (件)与时间
(件)与时间 (天)的函数关系是
(天)的函数关系是
 ,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是
,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是 天中的第几天?
天中的第几天?