已知椭圆 上的左、右顶点分别为
上的左、右顶点分别为 ,
, ,
, 为左焦点,且
为左焦点,且 ,又椭圆
,又椭圆 过点
过点 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)点 和
和 分别在椭圆
分别在椭圆 和圆
和圆 上(点
上(点 除外),设直线
除外),设直线 ,
, 的斜率分别为
的斜率分别为 ,
, ,若
,若 ,证明:
,证明: ,
, ,
, 三点共线.
三点共线.
设命题 :实数
:实数 满足
满足 ,其中
,其中 ;命题
;命题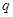 :实数
:实数 满足
满足 且
且 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.
已知集合 ,
, ,
,
求(1)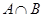 ;(2)
;(2) .
.
已知函数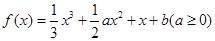 ,
, 为函数
为函数 的导函数.
的导函数.
(1)设函数f(x)的图象与x轴交点为A,曲线y=f(x)在A点处的切线方程是 ,求
,求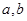 的值;
的值;
(2)若函数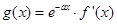 ,求函数
,求函数 的单调区间.
的单调区间.
在平面直角坐标系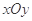 中,动点
中,动点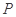 到两点
到两点 ,
, 的距离之和等于
的距离之和等于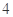 ,设点
,设点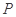 的轨迹为曲线
的轨迹为曲线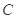 ,直线
,直线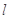 过点
过点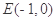 且与曲线
且与曲线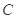 交于
交于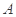 ,
,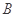 两点.
两点.
(1)求曲线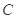 的轨迹方程;
的轨迹方程;
(2)是否存在△ 面积的最大值,若存在,求出△
面积的最大值,若存在,求出△ 的面积;若不存在,说明理由.
的面积;若不存在,说明理由.
设数列{an}的前n项和为Sn,且 ,n=1,2,3
,n=1,2,3
(1)求a1,a2;
(2)求Sn与Sn﹣1(n≥2)的关系式,并证明数列{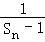 }是等差数列;
}是等差数列;
(3)求S1•S2•S3 S2011•S2012的值.