(本小题满分12分)某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组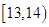 ,第二组
,第二组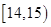 , ,第五组
, ,第五组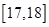 .右图是按上述分组方法得到的频率分布直方图.
.右图是按上述分组方法得到的频率分布直方图.
按上述分组方法得到的频率分布直方图.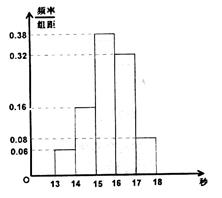
(Ⅰ)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(Ⅱ)设m,n表示该班某两位同学的百米测试成绩,且已知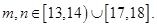 求事件“
求事件“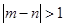 ”发生的概率.
”发生的概率.
(本题满分13分) 如图,在四棱锥 中,底面
中,底面 是菱形,
是菱形,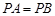 ,且侧面
,且侧面 平面
平面 ,点
,点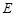 是棱
是棱 的中点.
的中点.
(1)求证: 平面
平面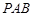 ;
;
(2)求证: ;
;
(3)若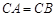 ,求证:平面
,求证:平面 平面
平面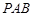 .
.
(本小题满分13分)已知函数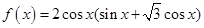
(1)求 的值域和最小正周期;
的值域和最小正周期;
(2)若对任意 ,使得
,使得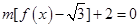 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分13分)已知数列 满足:
满足: ,数列
,数列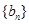 满足:
满足: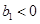 ,
, ,数列
,数列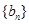 的前
的前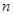 项和为
项和为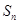 .
.
(Ⅰ)求证:数列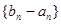 为等比数列;
为等比数列;
(Ⅱ)求证:数列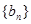 为递增数列;
为递增数列;
(Ⅲ)若当且仅当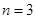 时,
时,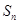 取得最小值,求
取得最小值,求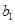 的取值范围.
的取值范围.
设 .
.
(1)令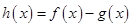 ,求
,求 的单调区间;
的单调区间;
(2)若当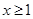 时,
时,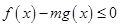 恒成立,求实数
恒成立,求实数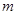 的取值范围;
的取值范围;
在平面直角坐标系xOy中,M、N分别是椭圆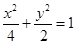 的顶点,过坐标原点的直线交椭圆于P,A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C,连结AC,并延长交椭圆于点B,设直线PA的斜率为k.
的顶点,过坐标原点的直线交椭圆于P,A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C,连结AC,并延长交椭圆于点B,设直线PA的斜率为k.
(1)若直线PA平分线段MN,求k的值;
(2)当k=2时,求点P到直线AB的距离d,且求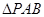 的面积
的面积 .
.