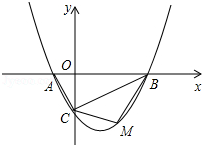
边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.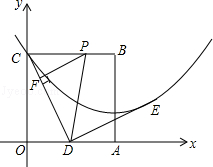
(1)求抛物线的解析式;
(2)点P从点C出发,沿射线CB每秒1个单位长度的速度运动,运动时间为t秒.过点P作PF⊥CD于点F,当t为何值时,以点P,F,D为顶点的三角形与△COD相似?
(3)点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.
某班级45名同学自发筹集到1700元资金,用于初中毕业时各项活动的经费.通过商议,决定拿出不少于544元但不超过560元的资金用于请专业人士拍照,其余资金用于给每名同学购买一件文化衫或一本制作精美的相册作为纪念品.已知每件文化衫28元,每本相册20元.
(1)设用于购买文化衫和相册的总费用为 元,求总费用 (元 与购买的文化衫件数 (件 的函数关系式.
(2)购买文化衫和相册有哪几种方案?为使拍照的资金更充足,应选择哪种方案,并说明理由.
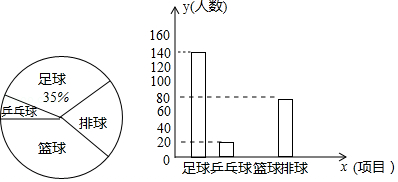
某校为提高学生身体素质,决定开展足球、篮球、排球、乒乓球四项课外体育活动,并要求学生必须并且只能选择一项.为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并绘制出以下两幅不完整的统计图.请根据统计图回答下列问题.(要求写出简要的解答过程)
(1)这次活动一共调查了多少名学生?
(2)补全条形统计图.
(3)若该学校总人数是1300人,请估计选择篮球项目的学生人数.
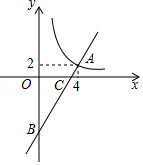
如图,一次函数 的图象与反比例函数 的图象在第一象限交于点 ,与 轴的负半轴交于点 ,且 ,
(1)求函数 和 的解析式.
(2)已知直线 与 轴相交于点 ,在第一象限内,求反比例函数 的图象上一点 ,使得 .
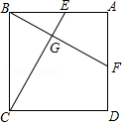
如图,四边形 是正方形, 、 分别是 、 上的一点,且 ,垂足为 ,求证: .
如图,抛物线 的图象与 轴交于 、 两点,与 轴交于 点,已知 点坐标为 .
(1)求抛物线的解析式;
(2)试探究 的外接圆的圆心位置,并求出圆心坐标;
(3)若点 是线段 下方的抛物线上一点,求 的面积的最大值,并求出此时 点的坐标.